고정 헤더 영역
상세 컨텐츠
본문
선형대수를 배웠거나 공학수학을 하다보면 eigen vector 를 많이 보았을 것이다.
간단히 말해서 A*x = b*x 의 경우에서
(A - b*I)*x=0 으로 정리했을때 이 식을 만족시키는 0이 아닌 A-b*I의 값이다. 즉 det = 0 인경우를 말한다.
고유치와 고유벡터를 매트랩으로 한번에 구할 수 있다

이때 v 행렬의 열이 바로 고유 벡터 들이고 d 행렬의 대각행렬이 고유치이다.
그리고 이 값을 얻게 해주는 특성 방정식의 계수 또한 구할 수 있다

poly 명령어를 사용해 주면 된다
2. LU 인수분해
어떠한 행렬을 가우스 소거법을 사용하여 upper , lower 삼각행렬로 분해 할 수 있다
A 라는 행렬이 인수분해 되는 식은
P*A = L * U 이다
매트랩으로 매우 쉽게 L U P 행렬을 다 구할 수 있다

A 행렬은 계속 같은 magic(3) 행렬이다
얻은 인수분해 된 행렬을 곱해보면 같게 나오는것을 확인 할 수 있다
3. 특이값 분해 SVD Decomposition
이 분해의 식은
A = U*S*V' 이다

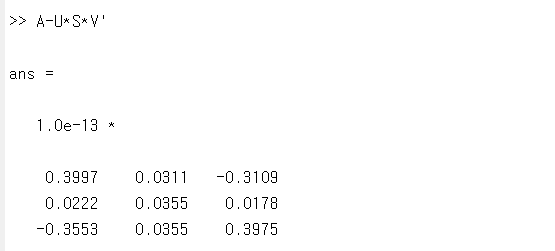
인수분해 된 행렬의 곱은 완전히 A 와 같은 행렬은 아니고 매우 근사한 행렬로 근사됨을 알 수 있다
4. 주성분 분석
어떠한 2개의 데이터를 두고 특정한 경향성이 있는가? 혹은 그것을 대표하는 값은 무엇인가? 를 근사할 수 있는 방법이
주성분 분석이다. 데이터 해석은 너무나도 방대한 영역이기에 자세히 다룰 수는 없고 , 후에 매트랩으로 데이터를 분석하
고 수정하는 기법을 따로 만들어서 해보도록 하겠다.
키와 몸무게의 데이터로 간단한 주성분 분석을 해보도록 하겠다

먼저 그래프에 점을 찍어내면 직선은 아니지만 어느정도 데이터가 경향성을 가진다는 것을 알 수 있다.
그렇다면 svd 인수분해를 이용하여 주성분을 분석해보자
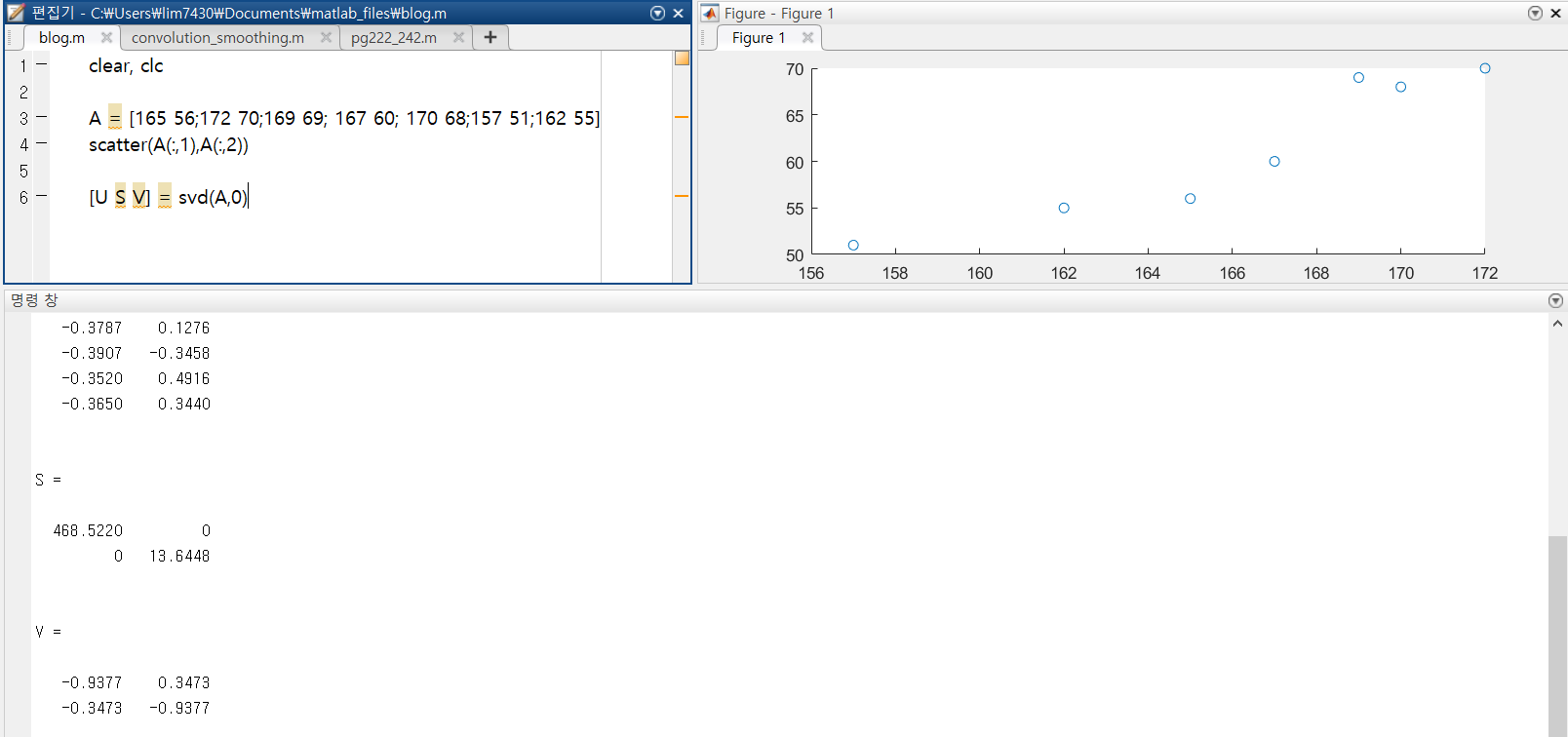
S 의 행렬로 sigma 행렬을 만들어주고 작은 값말고 큰값을 사용하도록 하자
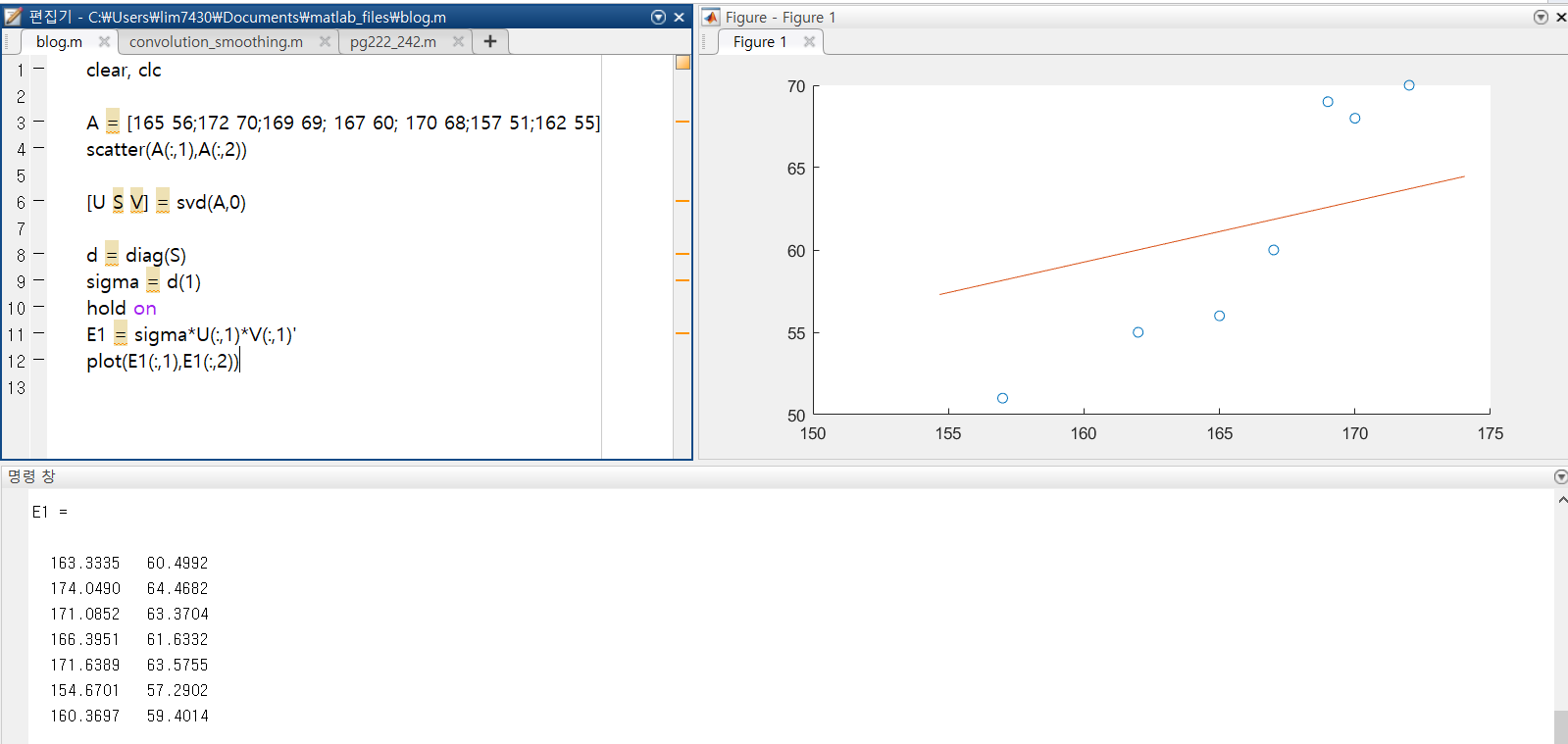
그렇다면 E1 의 데이터로 근사하고 그래프를 그려보면 어느정도 맞아 떨어지는 추세선을 그릴 수 있다.
이것 이외에도 Jordan , Schur 형태도 매트랩으로 할 수 있고
norm 과 조건수 또한 매우 쉽게 매트랩으로 구할 수 있다.
선형대수를 공부하고 있는 학생이라면 매트랩을 병행해서 공부하는것도 좋은 방법이 될 것 같다
'장.Matlab > Matrix - Linear Algebra' 카테고리의 다른 글
| Sparse Matrix (성긴행렬) (0) | 2021.01.31 |
|---|---|
| 행렬의 생성 (0) | 2021.01.31 |




댓글 영역