데이터 처리4 - curve fitting

 

이산적인 데이터를 가지고 추세를 파악하거나 계산 할 수 있는 근사한 방정식을 찾는것을 curve fitting 이라고 한다.

 

실제로 공학을 공부할때 마주하는 여러가지 식이 수학적으로 증명된 식이 아니고 실험을 기초로 하여 curve fitting을 

 

통해 유사한 식으로 만들어낸 실험식이 많다.

 

다양한 curve fitting 기법이 있지만 이번에는 기본적인 다항식으로 접합을 하는 방법과 내가 원하는 sine cosine 등 

 

초월함수도 이용하여 fitting 하는 방법에 대해서 알아보도록 하겠다.

 

코드가 조금 어려울 수 있지만 익숙해지면 쉽다. 그리고 추가적으로 매트랩 내에 아주 쉽게 curve fitting을 해주는 

 

기능도 있다. 

 

 

 

 

다항식을 이용한 fitting

 

polyfit 명령어로 내가 원하는 차수의 다항식의 계수를 구한다

 

이후 polyval 을 이용하여 치역을 구한다

 

간단한 예를 살펴보자

 

 

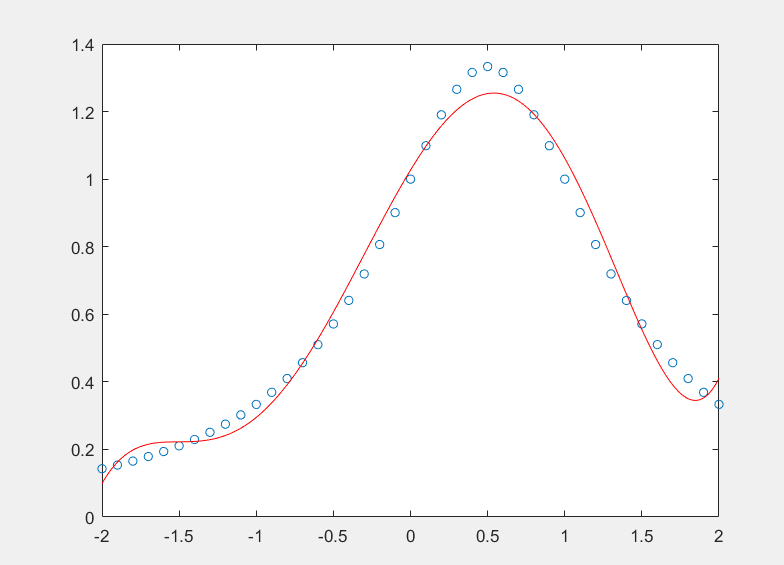
이렇게 다항식을 이용해서 curve fitting을 할 수 있다

 

 

 

이번에는 이전 포스팅에서 사용했던 count.dat의 데이터를 fitting 해보도록 하겠다

5차 다항식으로 fitting 해보도록 하자

생각보다 잘 안맞는다.

 

다항식의 차수를 더 높혀보도록 하자

 

훨신 낫다. 이렇게 차수를 변경해보면서 잘 맞는 곡선을 찾으면 될것같다.

 

 

그러나 이렇게 다항함수로 근사하는 방법말고 삼각함수를 이용하여 근사하는 방법도 있다

 

이 방법은 데이터를 행렬로 만들어서 행렬식으로 계산을 해야한다

 

기본꼴은 Y = A * X 이다

 

식은 a + bcos(2pi/8)(x-5.5) 라고 하자

 

그렇다면 이 식은 

 

[1 cos()] * [a ; b] 의 형태로 볼 수 있다

 

당연히 x 의 갯수와 맞게 행의 수를 맞춰주어야 한다

 

그리고 계수(a,b)는 역행렬을 곱해서 얻을 수 있을 것이다.

 

 

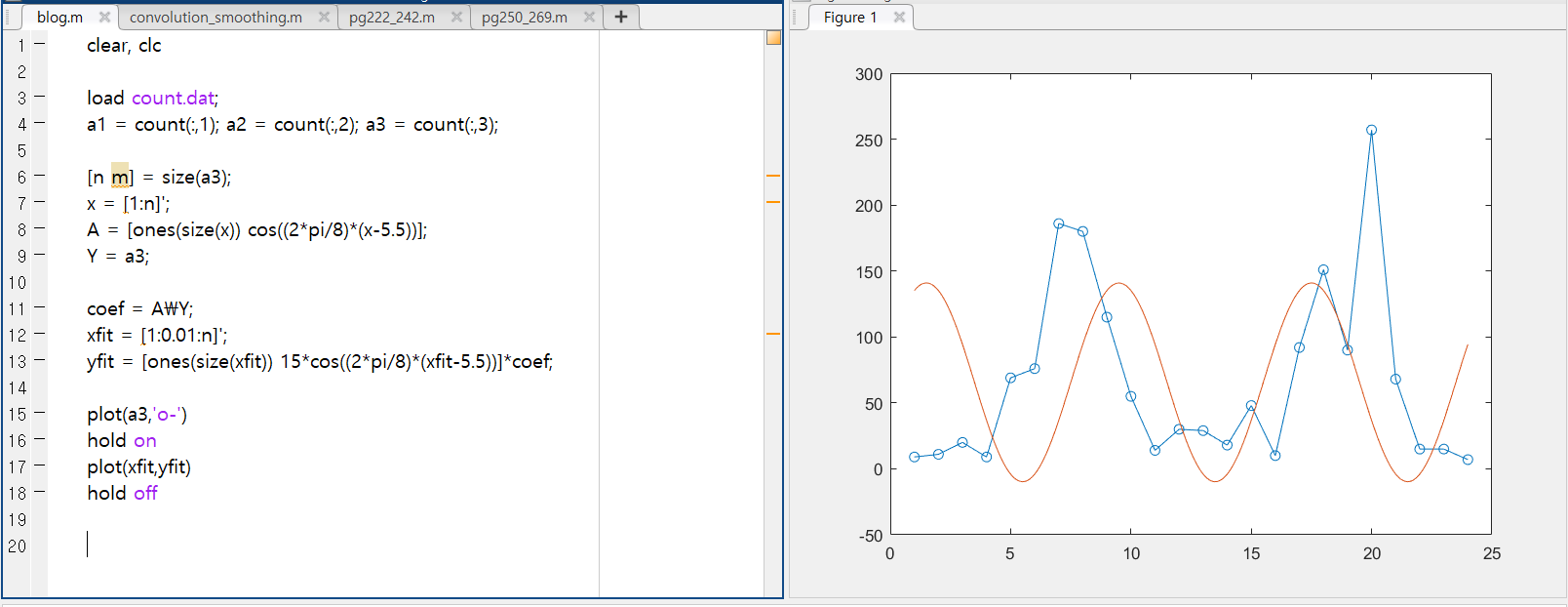
경우에 따라서 필요한 fitting 기법을 사용하면 좋을 것 같다