고정 헤더 영역
상세 컨텐츠
본문
1차 미분 방정식은 미분과 적분을 할 줄 안다면 큰 어려움 없이 계산 할 수 있는 식들이 많다.
그러나 2차 미분방정식이 나오고 경계치의 값들이 주어진 문제라면 이제 머리가 아파온다.
공학수학을 배울대 exp 함수를 이용하여 몇가지 정해진 형식으로 나누어 근을 구하고 했던 기억이 어렴풋이
날 것이다.
이렇게 손으로 풀 수 있는 방정식을 제외하고 그래프로 그리는 방법을 매트랩으로 연습해보도록 하자.
2차미분 방정식부터는 미분변수를 저장하는 형식을 익혀야 한다.
이제 2차미분이 나오면 matlab 에서는 아래와 같이 해석하도록 한다
y = Y1
dy = Y2 = dY1
d2y = dY2
이러한 관계를 염두해두고 dy 함수를 배열로 만들면 된다.
따라서 함수의 형태를
d2y = ~~~~ 꼴로 정리하여 풀이를 하도록 한다
예제를 살펴보자
식
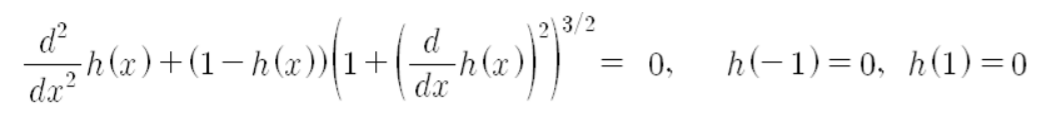
이러한 식을 아래와 같이 바꾸도록 한다

그러면 주어진 조건대로 미분 방정식을 풀어보도록 하자!

이렇게 경계치 문제를 풀어야 할 경우에는
3가지 부함수가 필요하다
1. 미분방정식의 함수
2. 경계값을 나타내주는 함수
3. 초기조건의 식 함수
그리고 해답을 얻는 과정은
bvpint 으로 초기조건의 mesh를 구하고
풀이는 ode45가 아닌 bvp4c로 구한다.
위의 코드를 따라서 작성을 하고 형식을 익힌다.
main 함수의 코드는 변하지 않는다. 상황에 따라서 달라지는 것은 3가지 부함수이다.
방정식과 조건에 따라서 3가지 부함수를 바꾸어주면 된다.
다른 예제를 하나 더 보자
식

초기가정은
sin(x) , cos(x) 이다

만약 위에 문제어서 u 와 같은 다른 변수가 하나 더있다면
초기 가정에서 그 변수의 값도 가정을 하고 풀이를 해준다
이번 방정식의 풀이도 main함수의 코드는 동일하다. 단지 plot을 위해 plot코드를 추가했을뿐 형식은 동일하다.
'장.Matlab > Differential Equation solver' 카테고리의 다른 글
| 미적분학4 - 접선 평면 근사 , 기울기 벡터필드 , 표면의 파라미터 표현 (0) | 2021.02.19 |
|---|---|
| 미분 방정식 5 - dsolve (0) | 2021.02.19 |
| 미분방정식4 - 편미분 방정식의 풀이 (0) | 2021.02.19 |
| 미분방정식2 - 상미분 방정식의 풀이 (0) | 2021.02.19 |
| 미분방정식1 - ode45 (1) | 2021.02.19 |




댓글 영역