Lecture 44. Bode's Rule, Stability Condition, Circuit example

-Important Point

 

1) If the Open Loop System satisfies K*H(j*Wo)=-1, then closed loop system is unsatble.

만약 Loop Gain에 해당하는 K*H(j*Wo)=-1이면 Closed Loop System은 불안정하게 된다. 

 

2) Even if X=0, the system still oscillate if K*H(j*Wo)=-1.

input이 없는 경우에도 해당 system은 oscillate 하게 된다. 그리고 이게 oscillator이다. 

 

3) What happens if |K*H(j*Wo)|>1 and <K*H(j*Wo)=180'?

K*H(j*Wo)의 magnitude가 1보다 크고 phase는 180도 인 경우 어떻게 될까?? 

즉 phase shift를 180도 시키고 크기가 1이 아닌 경우를 생각해보자. 

 

수식으로만 생각을 하게 되면 분모가 0이 아님으로 문제가 없을 것으로 생각할 수 있다. 하지만 이번 수업에서는 수식으로 따지는 게 아닌 그냥 직관적으로만 생각해보려 한다. 

위와 같이 X에 sinusoidal한 신호를 넣어주었다고 생각해보자. 기존에는 phase shift만 됨으로 K를 거친 후 input과 반대로 나타나기만 했는데 이제는 증폭되어 나타나게 된다. 이 상태로 subtract 하게 되면 더 크게 증폭이 됨으로 직관적으로 생각하면 이 또한 발산하게 될 것임을 알 수 있다. 그러므로 아래와 같이 조건을 수정할 수 있다. 

 

4) K usually has no pahse shift

K에서는 delay(~Phase shift)가 거의 없다. 그러므로 아래와 같이 생각할 수 있다. 

 

Bode's Rule 

 

- If we have a pole at Wp, the Phase of H(<H) experiences a change of -45' at Wp and -90' at ~10*Wp.

만약 Wp에서 pole frequency라고 하면 -45도의 phase 변화가 발생하고 약 10*Wp에서 -90도의 변화가 발생한다. 

그리고 10*Wp에서 -90도가 되는 것이 아닌 거의 -90도에 근사하는 값이 나온다. 

 

-If we have zero at Wz, then <H experiences a chage of 45' at Wz and 90' at ~10*Wz.

만약 Wz에서 zero frequency를 갖는다면 phase가 45도 증가하고 약 10*Wz에서 90도 증가한다. 

 

 

EX)

 

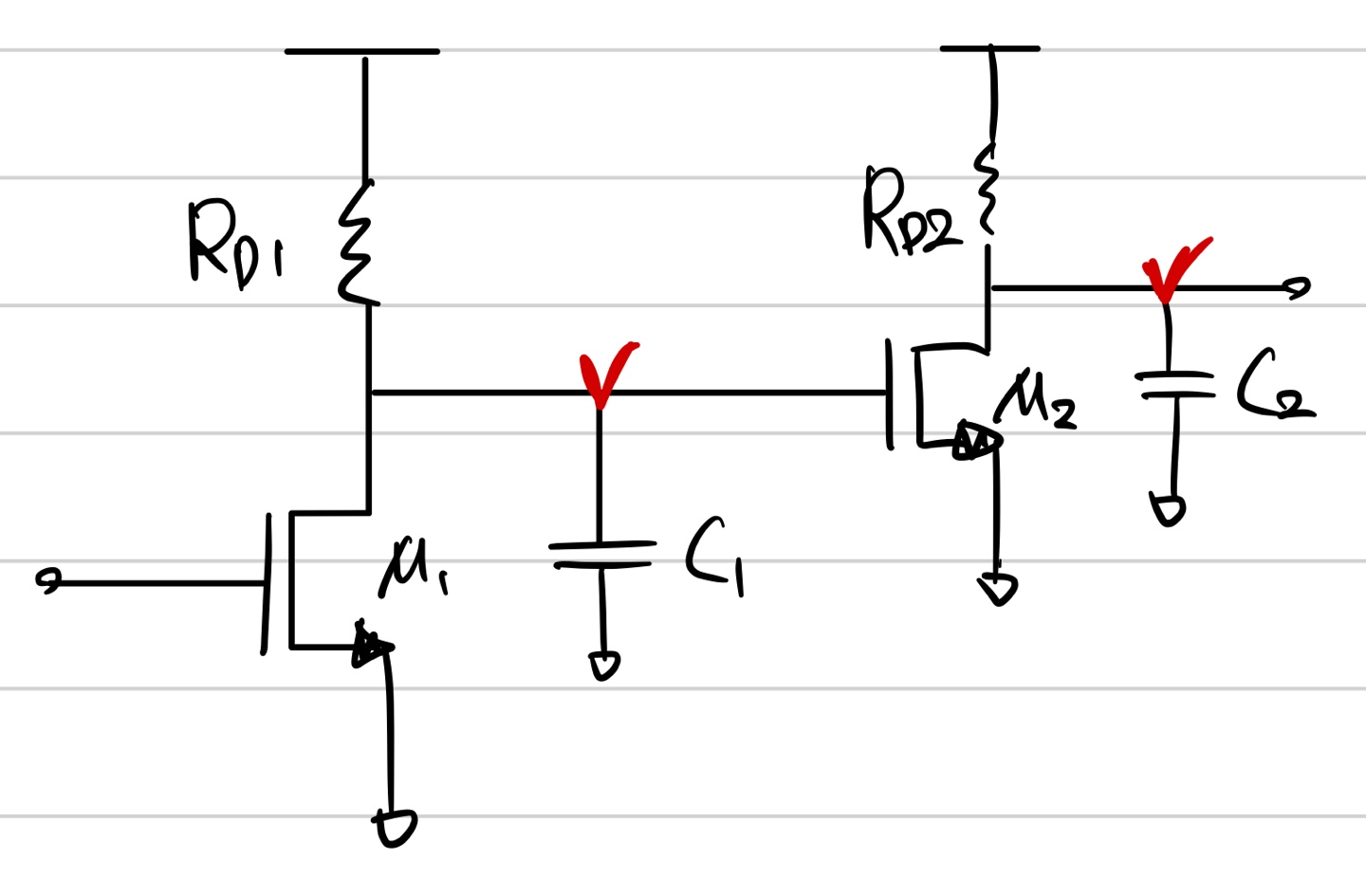
위와 같은 회로가 존재한다고 하자. 이때 pole은 두 개가 있음을 알 수 있다. 그리고 이때 magnitude와 phase를 보면 아래와 같다. 

두 개의 pole이 있으므로 magnitude는 -40db/dec까지 감소함을 알 수 있다. 그리고 phase의 경우 W가 무한대로 발산하게 되면 -180도에 도달함으로 oscillate하기 위한 조건을 만족하지 않고 있음을 알 수 있다. 10*/R2C2에서 -180도에 근접한 값이 나오게 되긴 하지만 -180도가 아니므로 위의 회로는 oscillate하지 않는다. 

 

W가 무한대로 가야 oscillate함을 알기 위해서 아래의 예시를 생각해보자. 

단순하게 pole이 하나인 transfer function을 생각해보자. 이때 G(s)의 phase를 구해보면 아래와 같다. 

real과 imagine의 관계를 이용해 위와 같이 구해줄 수 있다. 분모에 있으므로 부호가 음수이다. 이 값이 90도가 되려면 W/Wp가 무한대가 돼야 한다. 그러므로 10*Wp와 같은 값에서 90도보다 살짝 작은 값의 변화가 있는 것이지 90도가 아니다. 이를 통해 위의 예시에서 180도는 무한대로 발산할 때만 나타남을 알 수 있고 이는 해당 회로가 oscillate하지 않는다고 말할 수 있다. 

 

Stability Condition

 

위의 경우는 gain이 1이 되는 즉 0dB가 되는 frequency에서 phase가 -180도라고 가정해보자. 이 조건은 우리가 알고 있는 K*H(j*Wo)=-1에 해당한다. 그러므로 위와 같이 나오는 회로는 unstable하다. 

이번에는 W0에서 0dB이되고 W1에서 임의의 gain이 1보다 크고 phase가 -180도라고 가정해보자. 이때 gain이 1보다 크게 되면 이전에 봤듯이 positive feedback이 여전히 가능함으로 결과적으로 발산하게 된다. 그러므로 unstable 하다.

 

이번에는 Wo 0dB이 되는 frequency에서 phase가 -180도가 아니고 -180도가 될 때는 W1으로 0dB보다 작은 gain이 1이 안될 때이다. 이는 gain이 1보다 클 때는 -180도가 아니라서 oscillate하지 않고 180도가 돼도 gain이 1보다 작으므로 결국 수렴하게 된다. 그러므로 위와 같은 회로는 stable 하다. 

0dB가 되는 frequency를 Gain Crossover Frequency라 하고 -180도가 되는 frequency를 Phase Crossover frequency라 한다. 

그리고 이 조건을 만족할 때 해당 회로가 stable 하다고 말할 수 있다. 

 

EX)

위의 회로에서 A1에 해당하는 부분은 위와 같이 CS stage이고 여기에 C1으로 인해 하나의 pole이 있는 H(s)라고 가정해보자. pole이 하나 있으므로 magnitude를 살펴보면 아래와 같다. 

pole identification을 통해 대략 1/R1C1가 pole frequency임을 알 수 있다. 그리고 이때 bode's law에 따라 -20dB/dec만큼 감소하게 된다. phase를 살펴보면 

Pole이 하나임으로 -45도 감소 하고 10/RC에서 약 -90도로 나타나게 된다. 

 

이는 회로의 phase delay가 해봤자 90도임으로 oscillate하지 않는 stable 한 회로임을 확인할 수 있다. 

 

 

V/R

 

 

윤.