Lecture 9. Large-signal Model analysis of Bipolar Differential Pair

-Intuitive Study

Large signal model로 그리면 위와 같이 non linear한 그래프가 나오게 된다. 이를 바탕으로 전류에 대한 그래프를 생각해보면 아래와 같다. 

Ic1이 커지면 커질수록 Vx의 값이 감소하게 되고 Ic2의 값이 감소하면 Vy의 값이 감소하여 맨 위의 그래프 형태가 나옴을 알 수 있다. 

 

objective: Derive equations for Ic1, Ic2, Vx, Vy and Vx-Vy as a function of Vin1-Vin2

 

KVL을 이용하면 Q1과 Q2가 emitter에서 노드를 공유함으로 아래와 같이 식을 쓸 수 있다. 

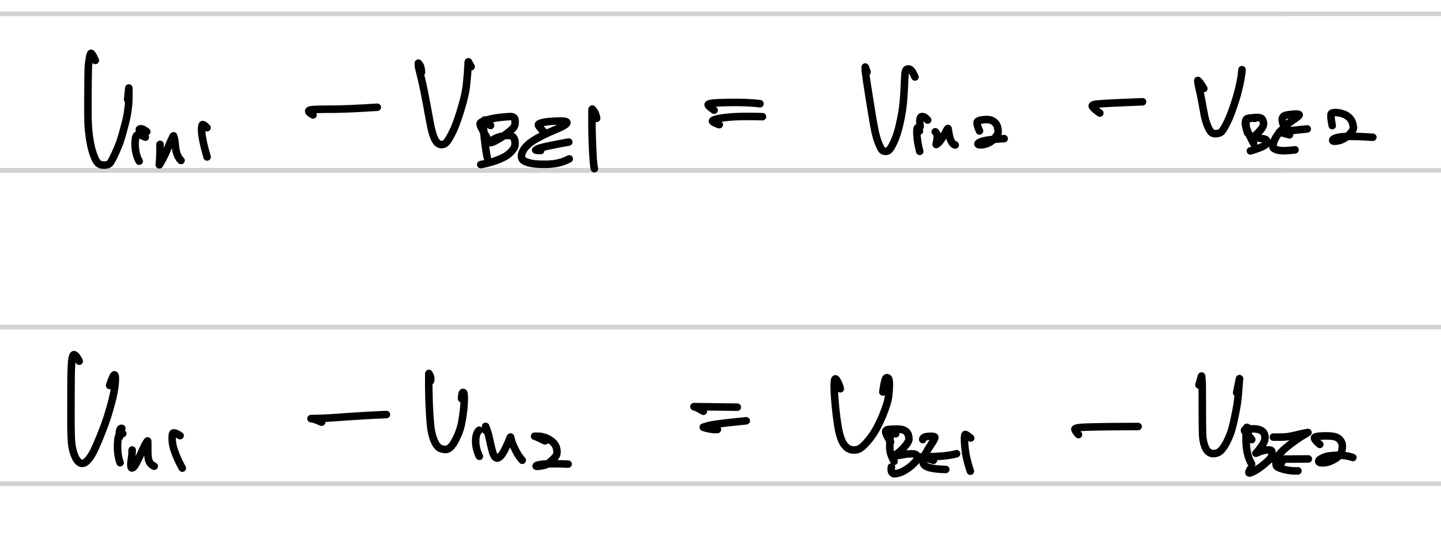
이때 Vbe는 bipolar transistor의 전류 공식을 이용해 아래와 같이 쓸 수 있다. 

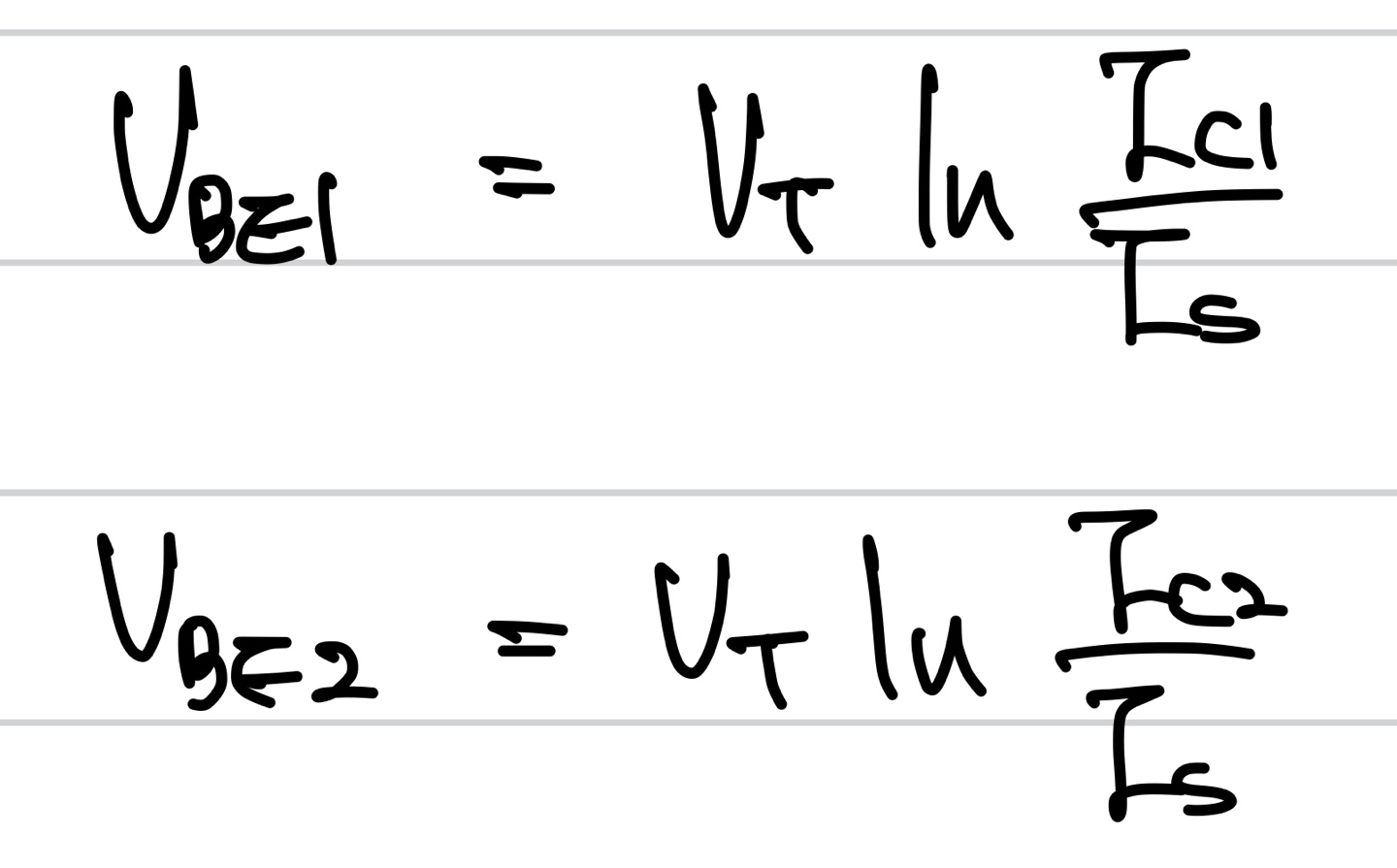
이를 이용해 아래와 같이 식을 쓸 수 있다. 

이때 전류에 대한 KCL을 적용하면 Ic1+Ic2= tail current 임으로 이를 이용해 아래와 같이 식을 정리해 줄 수 있다. 

여기서 Vin1과 Vin2가 같은 경우 exp의 값이 1이 되면서 Ic1이 tail current의 1/2의 값이 됨을 알 수 있다. 

Vin1-Vin2가 꽤 큰 경우에는 아래와 같이 식을 쓸 수 있다. 

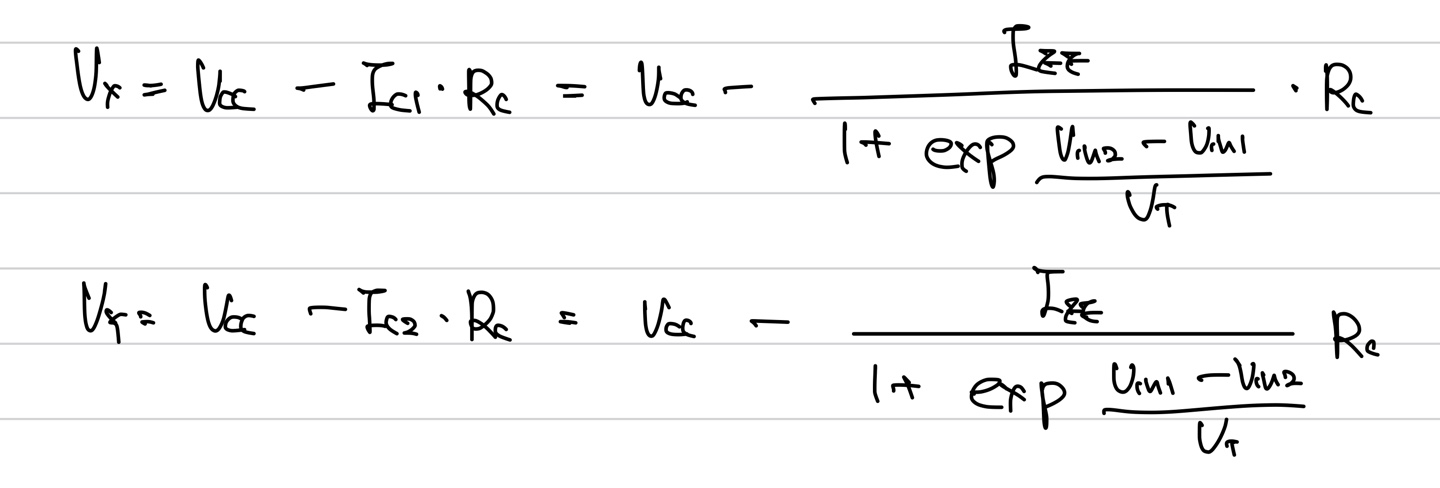
그래서 Vout의 값을 구해보면 아래와 같다. 

tanh의 그래프 개형을 보게 되면 이게 무슨 의미인지 생각할 수 있다. 

위의 그래프에 음의 상수가 곱해져 있으므로 아래와 같은 그래프가 그려지게 된다. 

 

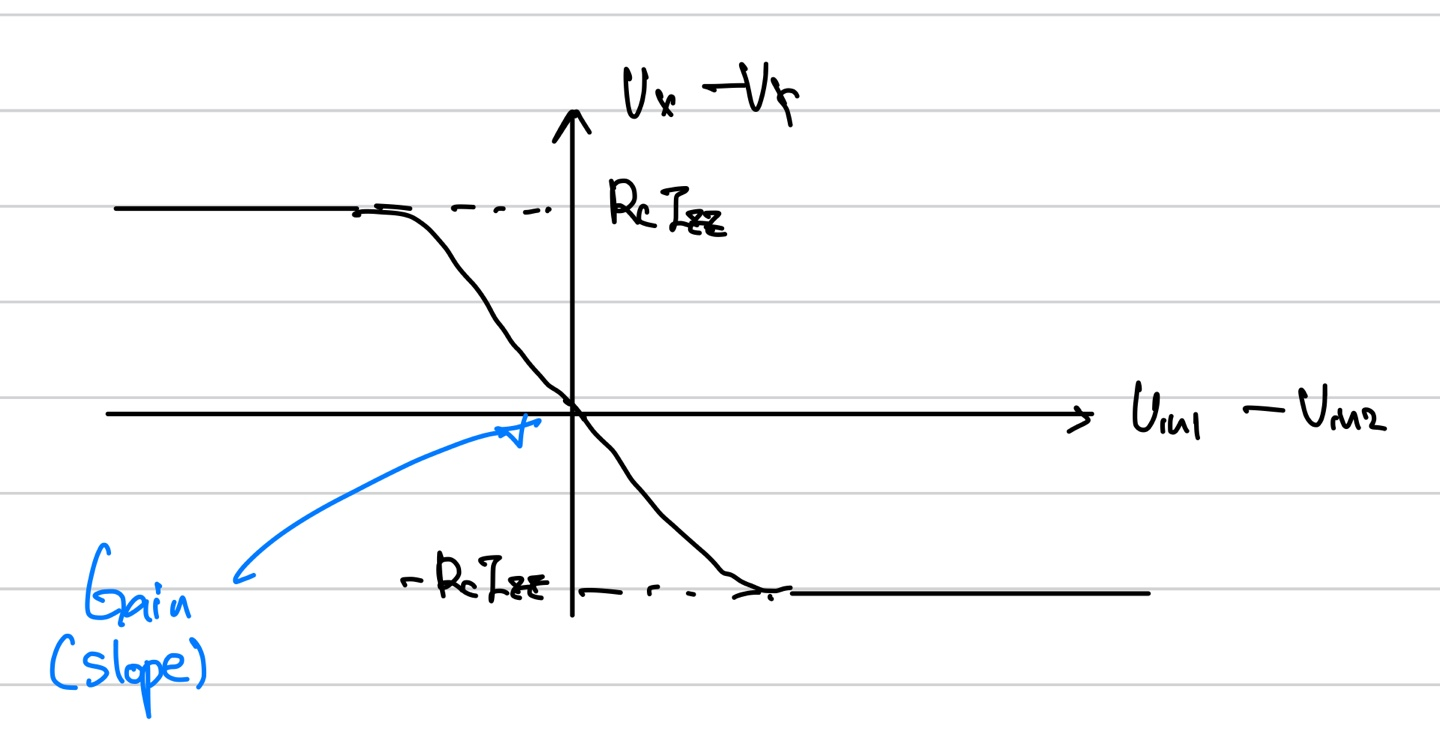
EX)

Find the slope of the characteristic around Vin1-Vin2=0

slope는 gain을 의미함으로 Vin1-Vin2 주변에서의 gain을 구하라는 의미이다. 

앞서 Vout에 대한 식이 tanh에대한 식으로 나타냈는데 이를 taylor function을 이용하여 정리하면 아래와 같다. 

이를 이용해 gain을 구하면 아래와 같다. 

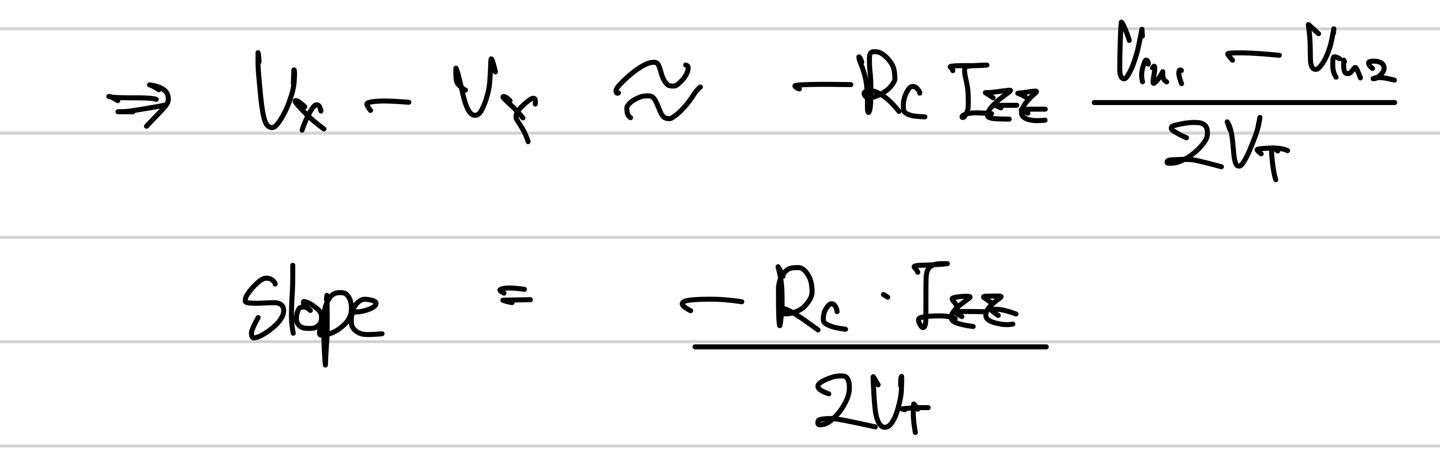
EX)

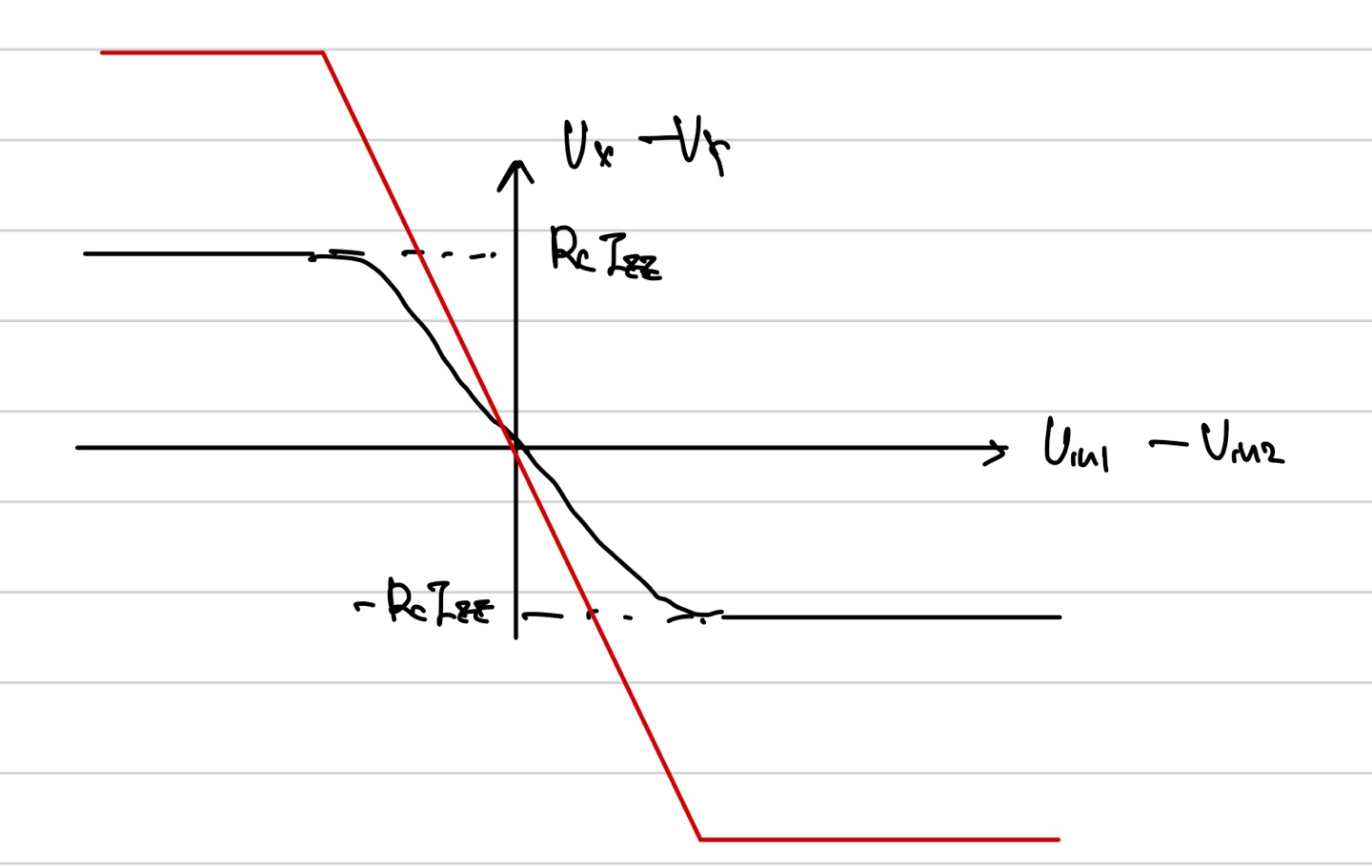
what happens to the characteristics if Iee is doubled?

tail current가 두배가 되면 기존의 Rc*Iee의 값이 두배가 됨으로 아래에서 빨간색 선과 같은 개형이 나타날 것이다. 

EX)

what happens if Rc is doubled?

Rc가 두배가 되면 앞서 한것과 똑같은 결과가 나오게 될 것이다. 

 

EX)

what happens if the ambient temperature drops considerably?

온도가 떨어지게 되면 어떻게 될까? 

앞서 slope의 값을 다시 살펴보자. 

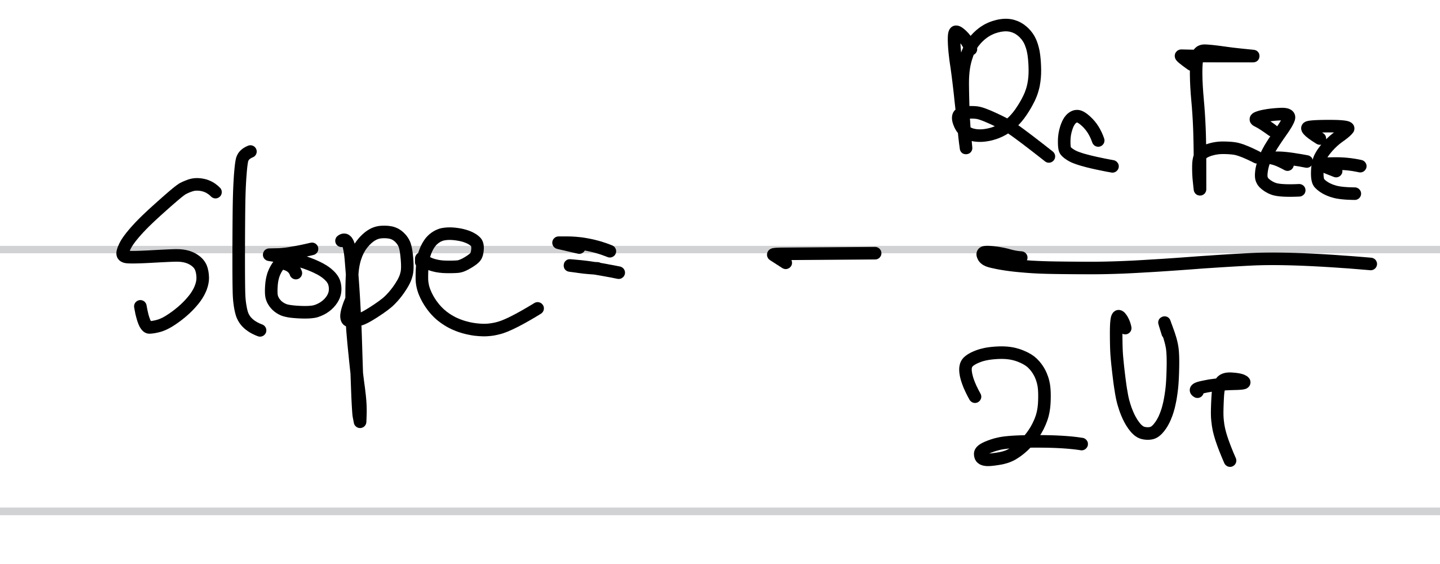
여기서 알 수 있듯이 분모에 온도에 따른 전압의 값이 존재하고 있다. 이는 온도가 낮으면 낮을수록 작은 값을 갖으므로 slope의 절대 값이 증가할 것임을 알 수 있다. 하지만 최대 값은 Rc*Iee로 결정됨으로 이 값은 변함이 없을 것이다. 그래서 아래에서 파란색과 같이 기울기는 늘어났지만 최댓값은 같은 그래프의 꼴로 나올 것이다. 

 

V/R

 

 

윤.