고정 헤더 영역
상세 컨텐츠
본문
-Small Signal Properties

이때의 Voltage gain을 구하기 위해서는 V1을 구해야 한다. KVL을 통해 Vin+V1=0임을 통해 V1=-Vin이라고 할 수 있다. 이때 KCL을 이용하면 아래와 같이 식을 정리할 수 있다.

이를 통해 Common Source Stage와 반대로 Av=gmRd임을 알 수 있다.
Rin을 구해보면 아래와 같다.

Common Gate에서 input이 source이다. 그러므로 위와 같이 small signal model에서 source에 test voltage를 연결했다. 그러고 나서 Vx+V1=0임을 KVL을 이용해 구해주고 KCL을 통해 식을 정리하면 Rin=1/gm임을 알 수 있다. 이는 앞서 common source에서 Rin이 무한대인 것에 비하면 매우 작은 값이다.
-Application
보통 amplifier에서 요구하는 Rin은 최대한 크게 Rout은 최대학 작게하는 것을 이상적으로 여긴다. 하지만 Common Gate stage에서는 Rin이 1/gm으로 상대적으로 매우 작다. 그럼 이게 왜 필요한지 살펴보자.
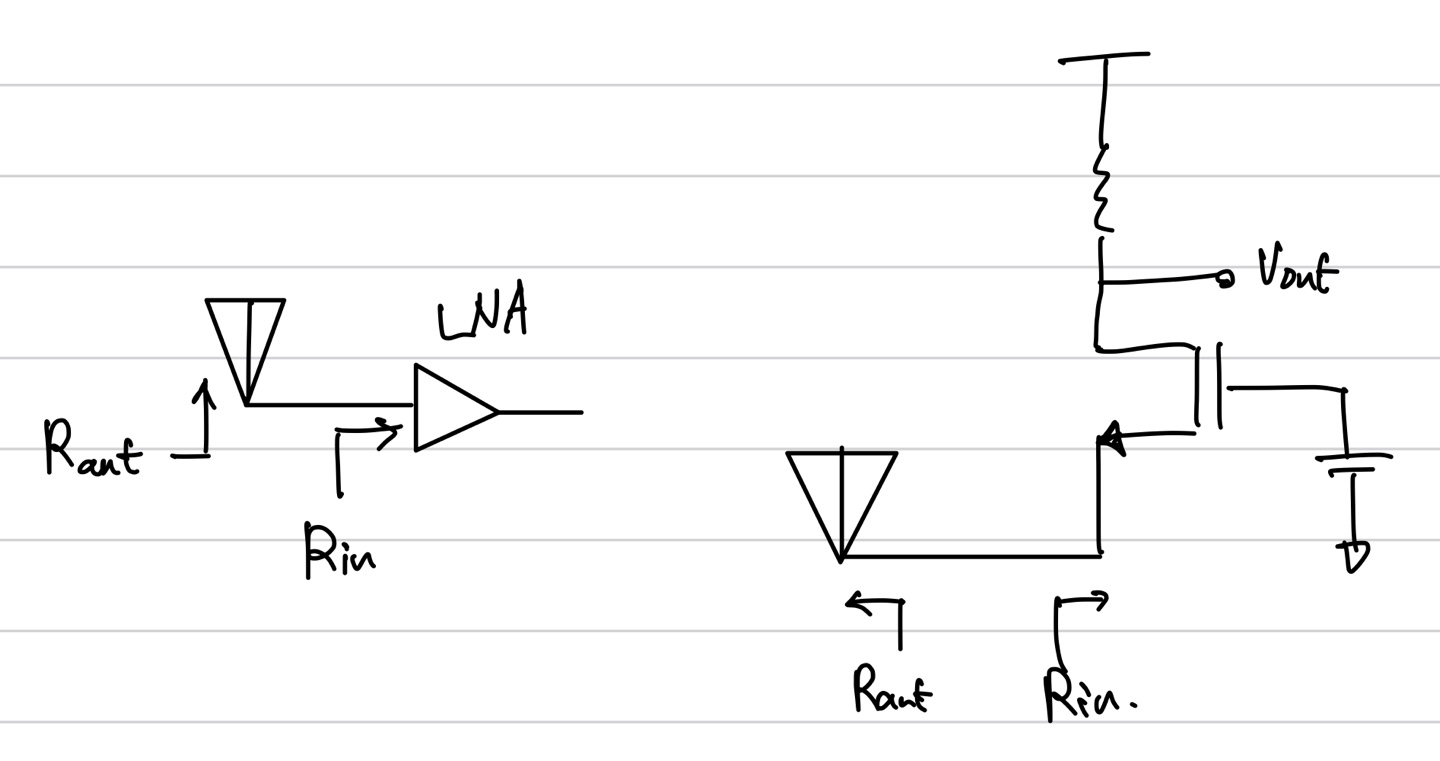
Reciever의 경우 왼쪽과 같이 회로가 구성된다. Antenna를 연결하고 Low Noise Amplifier를 거쳐야하는데 이때 Antenna의 내부 저항의 값을 생각해 봐야 한다. 안테나의 저항의 값을 50ohm이다. LNA가 CS stage를 사용하게 되면 Rin의 값이 안테나 저항의 값에 비하면 매우 높다. 즉 impedance matching을 만족시키지 못하게 된다. CG Stage를 사용하게 되면 Rin의 값이 작은 값이므로 impedance matching을 만족시킬 수 있게 된다. 이럴 때 CG Stage를 사용한다.
Rout

Rout을 구하기 위해서 부분적으로 ssm으로 나타내주고 test source를 연결해주었다. 근데 이를 잘 보면 CS Stage에서 Rout을 구할 때와 같음을 알 수 있다. 즉 Rout=Rd이다. channel length modulation을 고려하지 않았을 때...
Ex)

위의 회로의 voltage gain을 구하기 위해 Vout/Vin=Vx/Vin*Vout/Vx를 이용하여 구하면 된다. 이때 꼭 꼭 꼭 주의해야 될 부분이 M1의 drain 부분의 저항을 구할 때 M2를 고려해줘야 한다. R2를 생각하면 1/gm2이므로 아래와 같은 결과를 얻을 수 있다.

-Output Resistance of CG Stage in a special case
지금까지는 source에 Vin만 있을 때를 생각했는데 이번에는 Rs를 추가해 보자. 그리고 channel length modulation도 고려해보자.

위의 회로를 ssm으로 나타내면 오른쪽과 같다. 이때 Rout1과 Rout2로 나누어 생각하면 Rout1=Rd Rout2는 Rs가 1+gmro로 증폭된 값과 ro를 더해준 값으로 나타나게 된다. 이 두 저항이 병렬의 관계임으로 아래와 같은 결과를 얻을 수 있다.
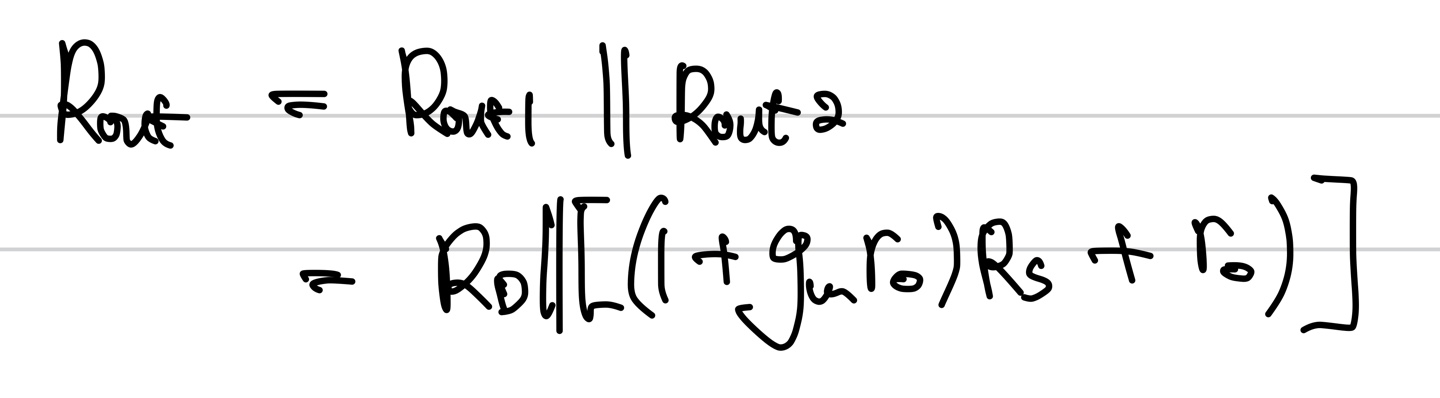
-Bias Design

이번에는 V-Antenna를 Vin으로 사용한 회로를 생각해보자. V-Antenna의 경우 DC에서는 OPEN이고 AC에서는 short상태인 Vin이다. 그럼 DC 상태에서 source가 open상태로 전류가 흐를 수 없으므로 오른쪽과 같이 Rs라는 저항이 필요로 한다. 하지만 이 Rs를 연결하게 되면 단점이 있다. 이를 살펴보기 위해 antenna의 내부저항을 고려해서 아래와 같이 회로를 그려보았다.

이렇게 되면 signal이 Rs로 흐르게 되면서 MOSFET으로 들어가는 i1만 증폭된다. 이러한 lose를 없애기 위해서는 i2를 매우 적게 하고 i1을 최대한 키워야 한다. 이렇게 하려면 Rs를 매우 크게 해야 한다. 이때 i1의 값을 구하려면 MOSFET의 source 저항 부분을 생각해 봐야 한다.

위와 같이 식을 얻을 수 있는데 이때 i1을 최대로 키우려면 Rs>>1/gm임을 다시 한번 확인할 수 있다.
이때의 voltage gain을 구해보자.

우선 gain을 구하기 위해 Vout/Vin=Vx/Vin*Vout/Vx를 이용하려고 한다. 우선 Vx/Vin을 구하기 위해 노란색 부분을 생각해보면 오른쪽과 같이 회로를 표현해 줄 수 있다. 그래서 이를 통해 아래와 같은 gain을 얻을 수 있다.

Ex)
Vdd=1.5V power budget=1.5mW UnCox=100uA/V^2 Vth=0.5V w/L=50 without channel length modulation
을 바탕으로 회로를 design해보자.
p=I*V=1.5mW로 Vdd=1.5V를 통해 I=1mA임을 알 수 있다. 이를 바탕으로 Id=1mA로 가정해보자. 이를 바탕으로 아래와 같이 Vgs를 구할 수 있다.

이 Vgs를 바탕으로 gm의 값을 구할 수 있다. 우선 우리가 거의 모든 조건을 갖고 있으므로 2Id/(Vgs-Vth)라는 식을 통해 구하면 아래와 같다.

Rs는 1/gm보다 커야 lose가 없으므로 단순하게 10*1/gm으로 하면 3.16kohm이다. 이렇게 되면 Source의 전압이 3.16V로 이렇게 되면 Vdd보다 큰 공급한 전압보다 큰 전압의 값을 갖게된다. 이렇게되면 안 됨으로 좀 더 생각을 해봐야 한다.
source의 전압의 값은 gate의 전압에 Vgs를 뺀 값이다. 이때 Id의 값이 constant한 상태임으로 source의 전압이 크려면 Rs의 값이 커야 한다. 그러므로 gate의 전압을 최대로 키워서 Vgs로 뺀 값이 최대 source 전압이고 이를 통해 구한 Rs가 최대 값이다. 그래서 gate 전압을 최댓값인 Vdd로 해주고 계산을 하면 아래의 결과를 얻을 수 있다.

그럼 이를 바탕으로 회로를 그리면 아래와 같다.

Rd를 구하기 위해 Vds>Vgs-Vth 조건을 사용해 보려 한다.

이를 바탕으로 voltage gain을 구하면 Av=gmRd=1.6이 나온다.
너무 낮은 gain이다...... 그럼 이를 높이기 위해서 어떻게 해야될까???????
이때 Vdd를 그대로 , Id의 값도 유지한 상태로 가정해보자.
그럼 무엇을 바꿀 수 있을까.... 바로 w/L을 바꿀 수 있다. 그럼 w/L을 두배로 100으로 만들어주면 어떻게 될까??

이를 이용해서 앞서 gate의 전압처럼 Vdd로 해주고 Rs를 계산하면 아래와 같다.

gm을 구하려면 아래와 같다.

Rs=550ohm 1/gm=220ohm으로 lose가 앞서 만든 회로에 비하면 lose가 훨씬 적을 것임을 알 수 있다. 이를 통해 gain을 구해보면 2.3으로 더 높은 gain을 얻을 수 있었다.
V/R
윤.
'윤. 전기전자 > MOS Transistor' 카테고리의 다른 글
| Razavi Ex7-15, 7-18, 7-19,7-20, 7-21, 7-22, 7-23 (0) | 2021.02.17 |
|---|---|
| Lecture 41. Source Follower (Common Drain) & Summary (0) | 2021.02.08 |
| Examples Common Source Stage (0) | 2021.02.07 |
| Lecture 39. Biasing Techniques, Intro. to Common Gate Stage (2) | 2021.02.06 |
| Lecture 38. Common-Source Stage with Degeneration (1) | 2021.02.05 |




댓글 영역