고정 헤더 영역
상세 컨텐츠
본문
오늘은 OpAmp를 다양하게 사용해보자
- Precision Rectifier
우리가 앞서 배운 rectifier는 다이오드를 이용하였다.

이때 Vin이 Vd,on을 넘기면 Vout으로 인식되고 그 이하의 전압은 D1이 OPEN 상태가 되어 흐르지 못한다. 그렇게 되면 아래와 같은 결과로 나타나게 된다.

Vin이 Vd,on보다 작은 값의 신호로 가정하면 Vout에서는 아무것도 인식하지 못하는 단점이 있다. 그럼 이를 해결하기 위해 OpAmp를 이용해 보자.

위와 같이 연결했을때 Ao가 매우 높다고 가정해보면 Vin=Vout이 된다. 이렇게 되면 Vin이 작은 값이어도 Vout에서 인식을 할 수 있게 된다. 그리고 Vin이 음의 값이 된다고 가정하면 Vout 또한 음의 값이 된다. 그렇게 되면 GND에서 Vout으로 전류가 흐르는 상황이 발생해야 되는데 이때 inverting input에는 전류가 흐르지 않고 다이오드 또한 반대로는 전류가 흐르지 못함으로 Vout이 0이 된다.

-Logarithmic Amplifier
말 그대로 로그 형태의 Vout을 얻게되는 회로를 말한다. 회로는 아래와 같다.

Virtual GND를 이용해 R1에 흐르는 전류값을 구하면 Vin/R1이다. 이 전류의 값은 Q1에 흐르는 전류의 값 Ic와 같으며 Ic=Is exp(Vbe/Vt)이다. Vbe=GND-Vout으로 대체해주어 계산하면 아래와 같은 결과를 얻을 수 있다.

이를 그래프로 나타내면 아래와 같다.

점선은 일반적인 Vin=Vout 일때를 그린 것이다. 일반적으로 amplifier를 이용할 경우 Vin이 높아져도 gain의 값이 일정하다. 하지만 logarithmic Amp는 Vin이 낮을 때 gain의 값이 크고 Vin이 높아지게 되면 오히려 gain의 값이 감소하는 형태로 나타난다. 그리고 수식에서 알 수 있듯이 Vin의 값이 언제나 양수가 되어야 한다. 그래서 Vin이 음수의 경우는 애초에 virtual GND에서 Vin으로 전류가 흐르는 즉 BJT 입장에서도 전류가 반대로 흐르는 상태가 되어야 하기 때문에 정의되지 않는다. 그래서 Vin이 음수의 경우를 알아보자
Quiz)

위의 회로에서 Vout/Vin을 구해보자. 방금 배운 회로와 다른점은 앞서 회로에서는 NPN을 사용했는데 이제는 PNP를 사용한다. 그래서 전류의 방향 또한 반대로 흐름으로 Vin이 음수여야 한다. 이번에도 virtual GND를 이용해 계산하면 아래와 같다.

-Op Amp Imperfections
지금까지 배운 Op Amp는 이상적인 경우로 Input에 전류가 흐르지 않고 Input resistance는 무한대이며 Ao도 매우 크고 output resistance는 매우 작다는 조건으로 배웠다. 하지만 현실에서는 당연히 차이가 존재한다.
1) Finite Gain
지금까지는 Ao를 매우 큰값으로 가정하여 Vin1=Vin2로 생각하여 쉽게 쉽게 풀었지만 당연하게도 Ao는 한계가 있다.
2) DC Offsets
이상적인 경우 Vin1=Vin2가 되면 Vout이 0이 된다. 하지만 현실에서는 이렇지 않다.
3) Input Bias Current
Input resistance가 무한일 수 없다. 물론 큰 값의 저항이겠지만 저항의 값이 아무리 커도 미세한 전류는 흐른다.
4) Finite Speed
이것은 gain이 증가하는 속도를 말한다고 해야되나 일단 나중에 설명하자.
gain에 대한 이야기는 상식적임으로 넘어간다.
-DC Offsets
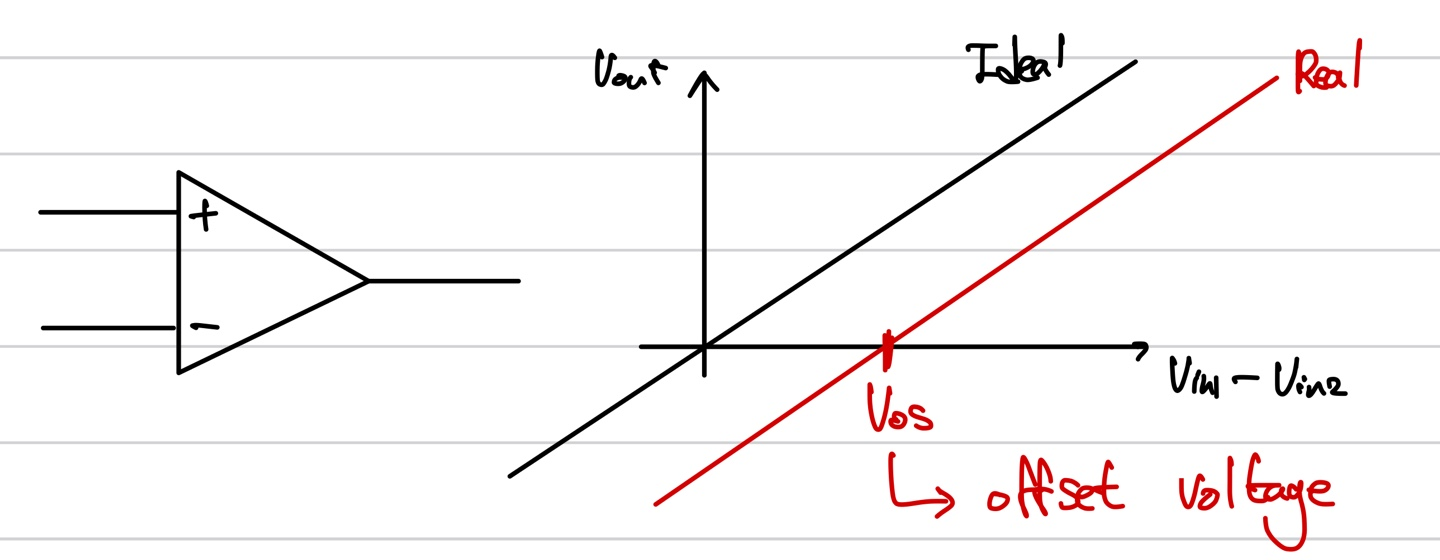
이론상 Vin1과 Vin2는 대칭적이다. 하지만 현실에서 공정의 과정에서 약간의 차이를 보일 수 있다. 그로 인해 Vout=0이 되는 지점이 바뀌게 되는데 이 값을 offset voltage라고 한다. 이를 아래와 같이 표현하여 고려해준다.

Observations
1) Offset Voltage is random
공정의 과정으로 생기는 오차임으로 통계적인 값은 있어도 정확한 오차의 값이 지정되어 있지 않다.
2) Vos can be placed in series with either Inputs (Vin1 or Vin2)
Vos의 값이 꼭 non inverting input에 연결되어야 하는 건 아니다 그냥 inverting input에 연결하고 Vos를 음의 값으로 해도 문제없다. 즉 편할 대로 연결하면 된다.
-Effects of Offset on Amplifiers
이제는 offset을 고려해서 close loop gain의 값을 구해보자
1) Non Inverting Amp

위와 같이 굳이 inverting input에 연결해 계산을 복잡하게 할바에는 non inverting input에 연결해 위와 같이 표현하였다. 그럼 전압의 값을 더해서 Vin1=Vin2를 사용하면 된다. 참고로 Vin1=Vin2를 그냥 사용하는 이유는 Vos 즉 offset에 대한 것을 밖으로 꺼냈기 때문에 굳이 당장은 오차를 따질 필요 없다. 이를 바탕으로 아래와 같은 결과를 얻게 된다.

여기서 신기한점은 Vos또한 증폭된다는 점이다.
2) Inverting Amplifier

이번에는 Vos를 굳이 저항들 있는 곳에 연결하면 계산이 불편할 듯하여 non inverting input에 연결해 주었다. 그럼 이번에는 이 두 가지를 다 생각해보기 위해 superposition(중첩)을 이용하려 한다.
a) Vin=0인 경우

Vin이 0으로 short 시키면 위와 같이 회로를 보기 좋게 그려줄 수 있다. 이는 우리가 앞서 배운 non inverting amp의 이상적인 형태이므로 Vos가 증폭되게 된다.
b) Vos=0인 경우
이 또한 굳이 크게 생각할 필요 없이 inverting amp의 gain의 값을 사용하면 된다.
이 두 경우를 합치게 되면 아래와 같이 나온다.

이번에도 Vos의 값이 증폭된다. 이렇게 되면 우리가 원래 얻으려는 Vin의 값을 얻지 못할 수 있다. 이에 대한 해결책은 다음시간에.... ㅎ
V/R
윤.
'윤. 전기전자 > Op Amp' 카테고리의 다른 글
| Lecture 45. OpAmp Nonidealities 2 (0) | 2021.02.23 |
|---|---|
| Lecture 43. Op Amp Circuits 2 (0) | 2021.02.23 |
| Lecture 42. Op Amp Circuits 1 (0) | 2021.02.22 |




댓글 영역