고정 헤더 영역
상세 컨텐츠
본문
-Cascode Amp
우선 저번 글에서 배운 것에 대해 복습을 해보자.

이전 글에서 배웠듯이 Gm의 값을 구하면 gm임을 알 수 있다. 그리고 Rout의 경우 ideal current source가 drain에 연결되어 있으므로 ro만 고려하면 되어 위와 같은 결과를 얻게 된다. 그럼 이번에는 cascode된 경우를 살펴보자.

Vout을 AC GND로 만들고 Iout을 흐르게 하여 Gm을 구해보면 아래와 같다.

M1에 흐르는 전류의 값과 M2에 흐르는 전류의 값은 같다. 하지만 엄밀히 따지자면 ro2가 M2에 존재하고 현재 source가 GND 임으로 ro2가 M2와 병렬적으로 연결되어 있어서 전류가 온전히 같다고 말할 수는 없다. 그래도 나중에 설명하겠지만 거의 같은 값이 흐르기 때문에 Iout을 gm2*Vin으로 해줄 수 있다. 그 결과 Gm=gm2가 된다.
이를 바탕으로 Rout을 구하여 Av를 구하면 아래와 같다.

Quiz)

앞서 말한 전류에 대해 이야기 해보려 한다. ro2는 source와 drain에 연결되어 있는데 여기서 source가 GND가 연결되어 있으므로 ro2는 위와 같이 표현될 수 있다. 우리는 전류가 ro2가 아닌 M1으로 흐르길 원한다. 그래서 Req과 ro2의 값을 비교해보자. Req를 구해보면 아래와 같다.

이를 ro2와 비교해보면 일반적으로 gm*ro>>1의 관계를 갖는데 이 같은 관계를 갖는 이유는 gm*ro가 intrinsic gain으로 최대 gain을 나타내기 때문이다. 그래서 M1과 M2가 다르다고 해도 적어도 ro2의 값이 1/gm보다는 크다고 말할 수 있으므로 앞서 가정했던 것과 같이 ro2에는 전류가 적게 흐르고 M1에 전류가 더 많이 흐른다고 말할 수 있다.
EX)

이번에는 ideal current가 아닌 Rd가 있을때의 gain을 구해보자.
우선 Gm을 구하기 위해서 Vout을 AC GND로 만들고 부분적으로 small signal model을 적용하면 아래와 같다.

여기서 Rd의 경우 양쪽 node가 GND임으로 무시할 수 있다. 그리고 앞서 본 것처럼 ro2에는 전류가 적게 흐름으로 gm2*Vin=Iout이라고 말할 수 있다. 이제 Rout을 구하면 아래와 같다.
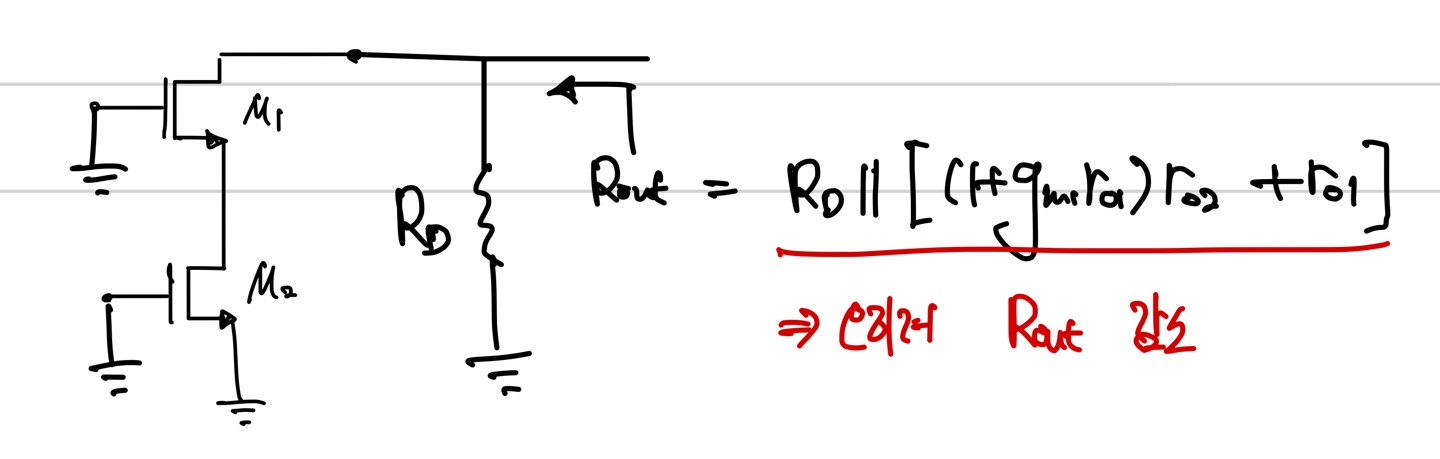
여기서 알 수 있는 것은 cascode로 기껏 올려둔 Rout이 Rd와 parallel하게 되어 감소하게 되는 결과를 보이게 된다는 점이다. Av는 이 두 값을 곱하고 -를 붙이면 된다.
-Cascode Amp with Current Source Load
앞서 Rd를 연결했는데 이번에는 current source를 대신 연결하면 아래와 같은 결과가 나오게 된다.

M3는 current source로 ro3로 치환하여 생각할 수 있다. M1과 M2의 Rout과 ro3가 병렬관계임으로 위와 같은 값이 나오게 된다. 그리고 ro3의 경우 이전의 예시에서 Rd와 같이 양끝이 GND가 되어 무시할 수 있게 된다.
-Cascode Amp with Cascode Load

Gm의 경우 앞서 한것과 같이 Vout을 AC GND로 만들고 Iout을 흘려준다. 이때 M3와 M4에 의한 load의 경우 앞서 Rd로 치환하여 다 없어진다고 생각하면 Gm=gm2라는 것을 쉽게 알 수 있다. 이제 Rout은 R1과 R2로 나누어 생각을 해보자. 그럼 PMOS의 경우 좀 어색할 수 있지만 위와 같은 결과가 나옴을 쉽게 알 수 있다.
-Bipolar Cascode Amp
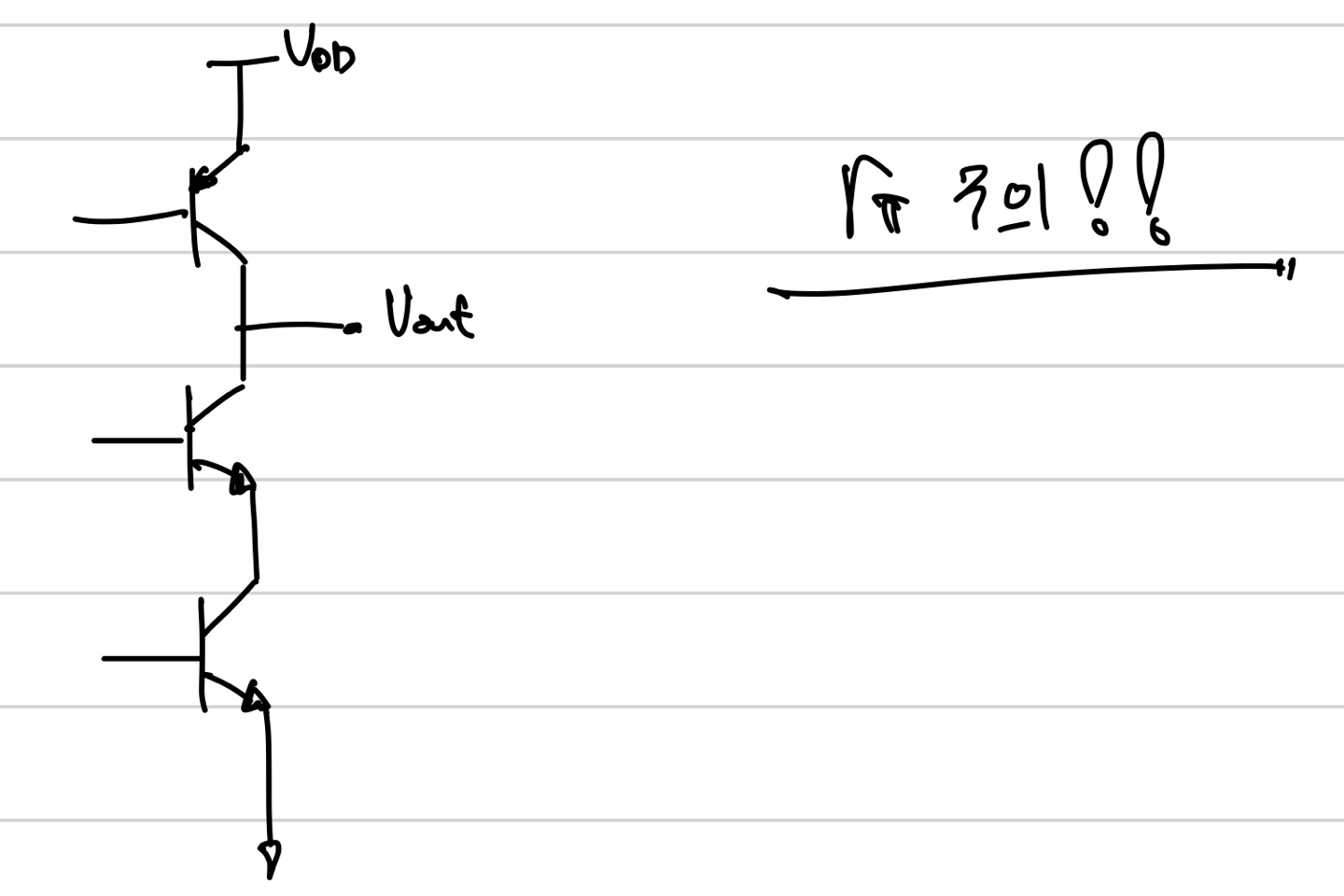
앞서 한것과 비슷함으로 rpi를 조심하자만 생각하고 넘어가자.
Question)

해당 회로의 Av를 구해보자. 우선은 Gm을 구하면 아래와 같다.

Rout은 앞서 구한 것과 같이 구해주면 아래와 같다.

V/R
윤.
'윤. 전기전자 > Cascode' 카테고리의 다른 글
| Lecture 4. Additional Cascode Examples, Cascode Amp with PMOS input (0) | 2021.07.08 |
|---|---|
| Lecture 2. MOS and Bipolar Cascode Current Source, Intro. to cascode Amplifier (0) | 2021.07.07 |
| Lecture 1. Cascode Current Source (0) | 2021.07.07 |




댓글 영역