고정 헤더 영역
상세 컨텐츠
본문 제목
Lecture 22. Dominant Pole Approximation, Response of CE/CS & Common Base/Gate stage
본문
이전 글에서 구한 transfer function은 아래와 같다.
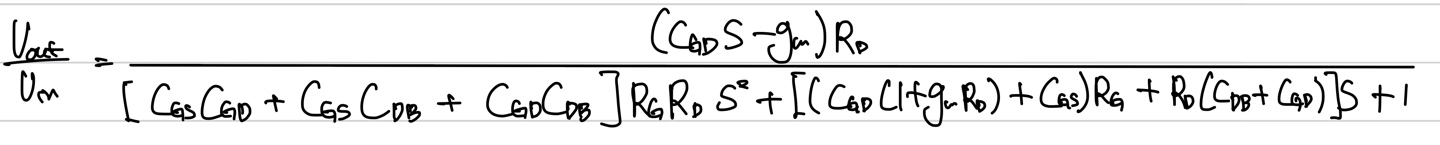
이제 Dominat Pole Approximation을 분모에 대해 적용을 해보자. 이때 Dominat Pole Approximation을 한다는 것은

위의 식에서 Wp1<<Wp2라고 가정해보자. 이렇게 되면 Wp1이 dominat pole이 된다. 그 이유는 pole frequency의 값이 작을수록 pole이 먼저 적용되기 때문이다. 즉 원점에서 더 가까움으로 이 pole과 원점 사이의 거리를 Bandwidth로 생각할 수 있다. 그래서 이를 dominant pole이라고 한다. 그래서 앞서 Wp1<<Wp2를 이용하면 위의 식에서 s의 계수에서 1/Wp2의 값을 무시할 수 있게 된다.
-> s의 계수의 값을 이용해 1/Wp1의 값을 구할수 있고 이를 이용하면 처음에 구한 transfer function에서 적용하면

그리고 s^2의 계수는 Wp1*Wp2임으로

이를 이용하면 Wp2의 값을 구할 수 있다.
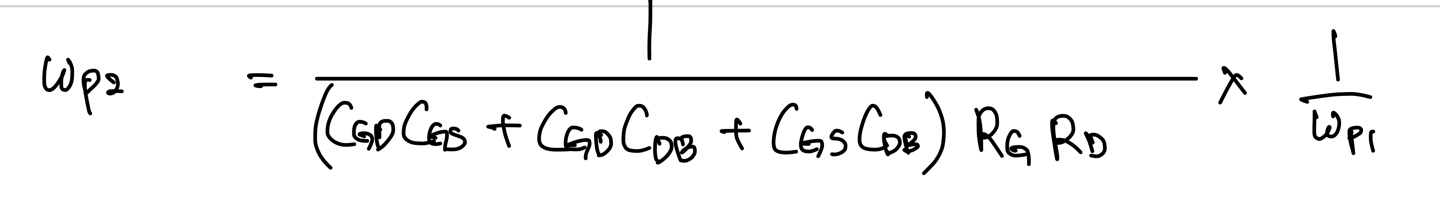
이를 이전에 pole inspectrion으로 구할때와 비교하면
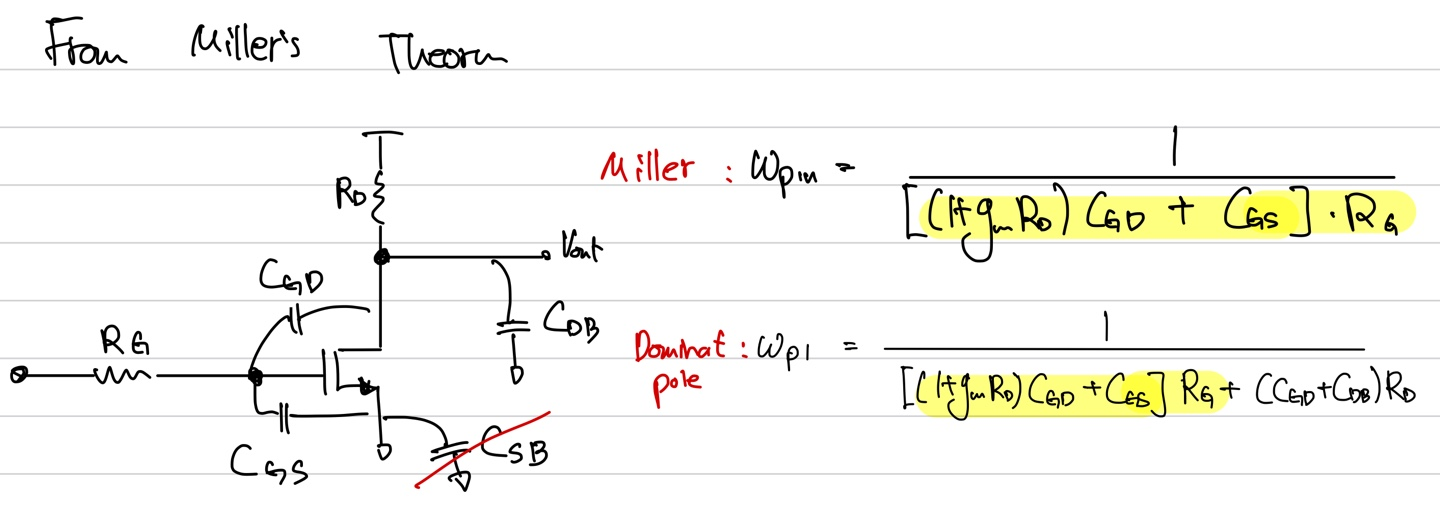
위의 값은 miller's approximation이고 아래는 dominat pole을 이용해 exact approach한 결과이다. 둘의 값이 완전히 같은 값은 아니지만 적어도 비슷한 경향을 갖는 값이라고 말할 수 있다.
A Few Points
1) if S=0

s=0일때 gain이 위와 같다고 하자.
2) if s=무한대

gain의 값이 0이 된다고 하면 이 두 가지를 고려했을 때 해당 transfer function은 low pass filter에 대한 함수이다. 이와 같은 방식으로 해당 회로에 대한 정보를 예측해 볼 수 있다.
3) 현재 우리는 3개의 cap이 있을 때를 생각하여 계산을 진행하였고 Second Order Response를 얻었다. 이를 통해 N개의 cap이 존재한다면 딱히 더 줄일 수 없는 상태일 때 N-th order differential equation을 얻을 수 있음을 알 수 있다.

그래서 이를 풀어주기 위해서는 N개의 독립적인 initial condition을 필요로 한다.
현재 Cgs, Cgd, Cdb 가 서로 연관이 되어 있으므로 second order equation이 나오게 된다.
EX)
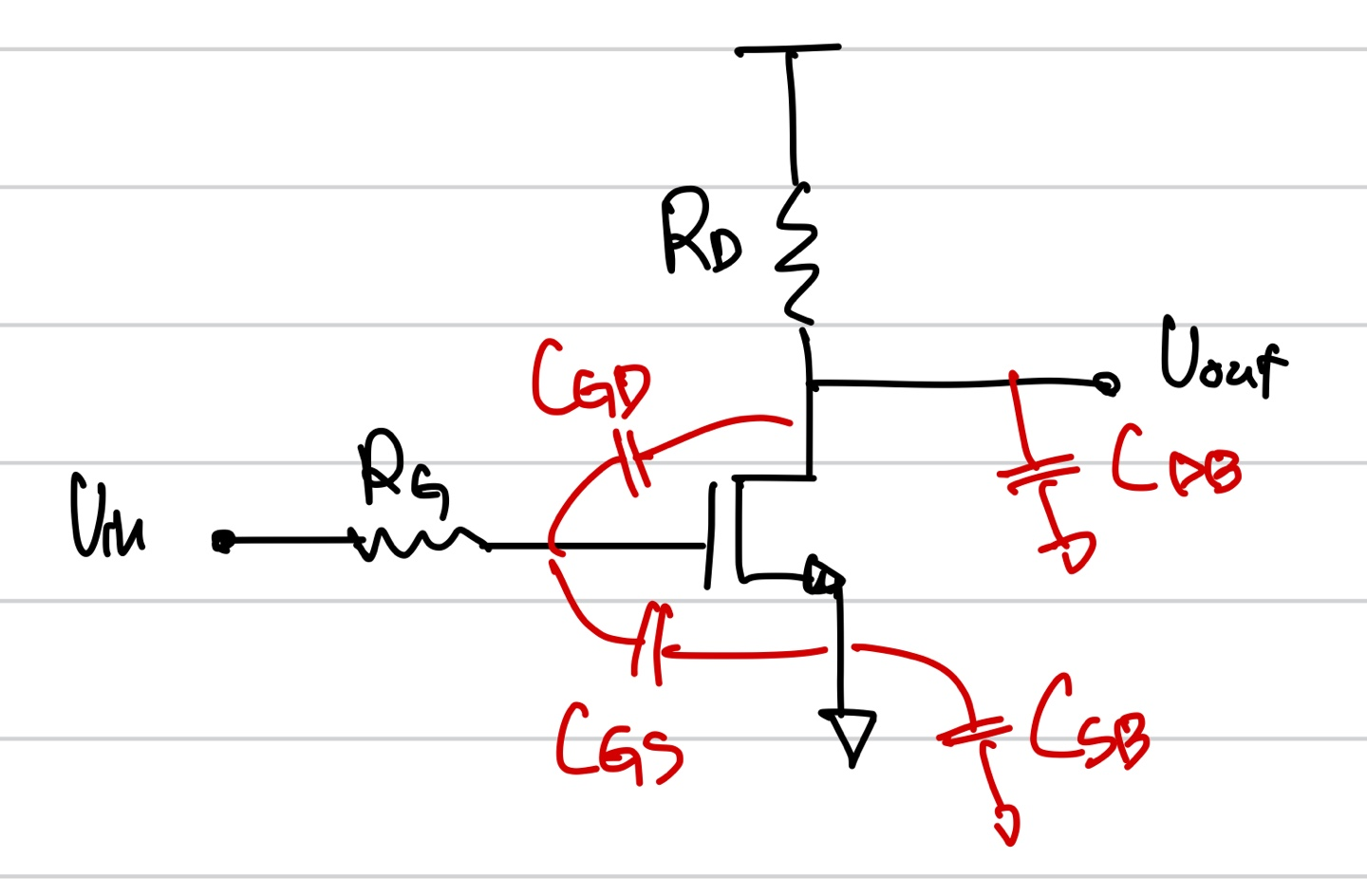
위의 회로에서 Width가 두배가 되고 전류의 값이 일정하면 어떻게 될까?????
이전에 W를 2배로 늘리게 되면 transistor를 병렬로 연결한 것과 같다고 했다. 아래와 같이 생각할 수 있다.
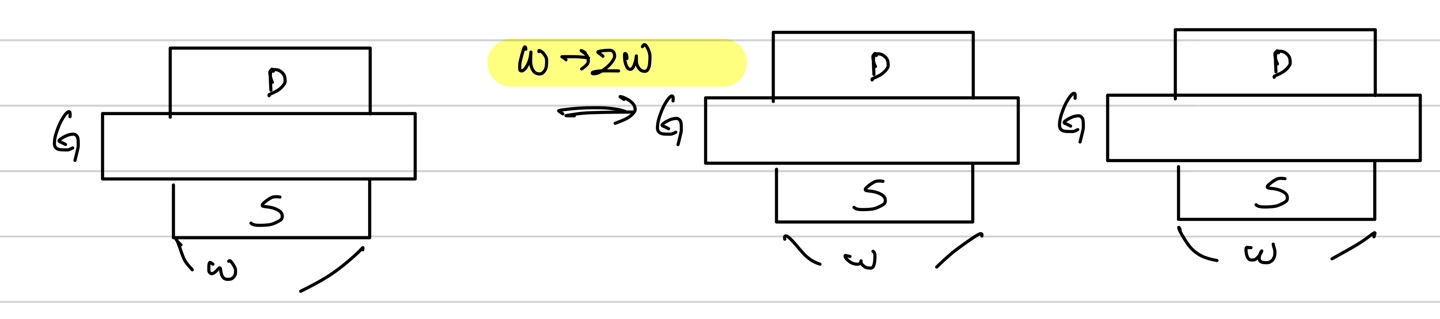
이를 회로로 그리면 아래와 같다.

이렇게 되면 위의 그림처럼 parasitic cap들이 병렬의 관계로 존재하게 됨을 알 수 있다. 즉 이전의 w였을 때 보다 capacitance의 값이 두배로 증가하게 된다.
이를 통해서 L의 값이 일정하다고 할때 W의 값을 조절하여 parasitic capacitance의 값을 조절할 수 있음을 알 수 있다. 그래서 회로를 설계하는 과정에서 혹시 pole의 값을 조절할 때는 W의 값을 낮추어 parasitic cap의 값을 낮추어 영향을 줄이는 것을 추천한다.
그래서 gm의 값을 구하면 아래와 같다.
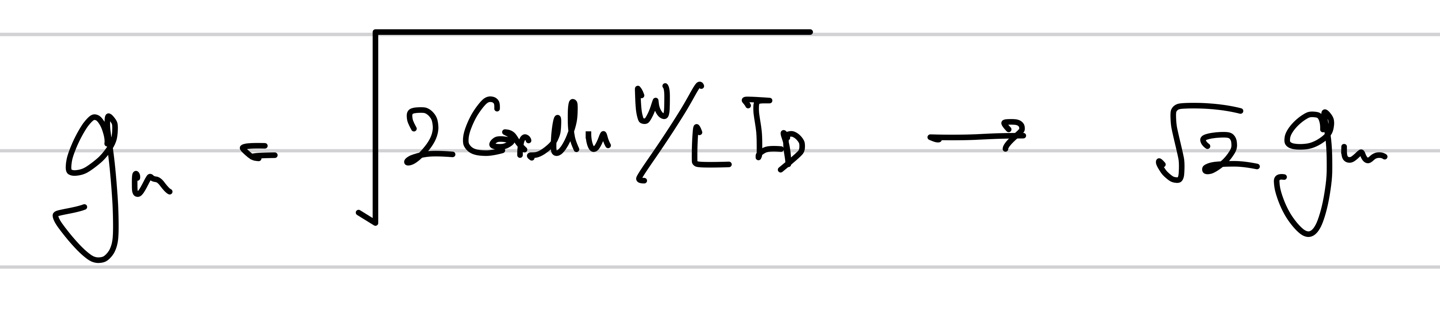
이를 바탕으로 Wp1의 값을 다시보면
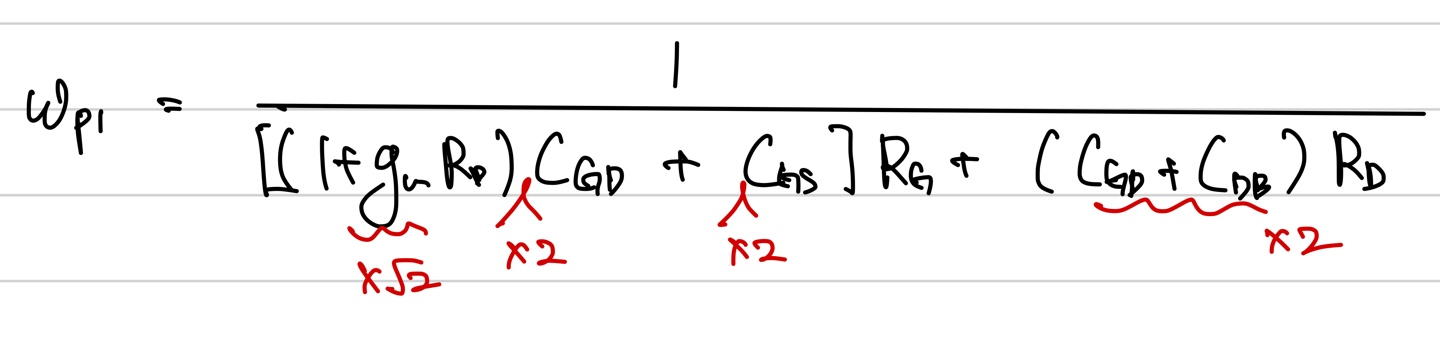
gm의 값이 루트 2배만큼 늘어나고 각각의 parasitic cap들의 값이 2배로 늘어나게 된다.
그 결과 Wp1의 값은 기존의 값보다 거의 2배 정도 감소하게 되고 이는 bandwidth의 감소로 이어진다.
그리고 gm의 값이 바뀌면서 gain의 값이 바뀌게 되고 이는 아래와 같이 그래프로 표현할 수 있다.

그래서 여기에서 알 수 있는 것은 w를 늘리게 되면 gain의 값이 증가하지만 한편으로는 parasitic capacitance 값이 증가하면서 Wp1의 값을 감소시키고 그 결과 bandwidth가 감소하고 있음을 확인할 수 있다.
다시 한번 나를 위해 다시 쓴다. Width를 키우게 되면 혹은 transistor를 병렬로 더 많이 연결하게 되면 gm*Rd에서 gm의 값이 증가하면서 gain이 증가하게 된다. 하지만 병렬로 연결된 transistor의 parasitic cap 또한 병렬 관계가 되어 parasitic capacitance의 값이 증가하게 되고 이는 Wp1의 값을 감소하게 한다. 그 결과 bandwidth가 감소하게 된다. 이를 통해 gain과 bandwidth가 tradeoff 관계임을 알 수 있다.
EX)
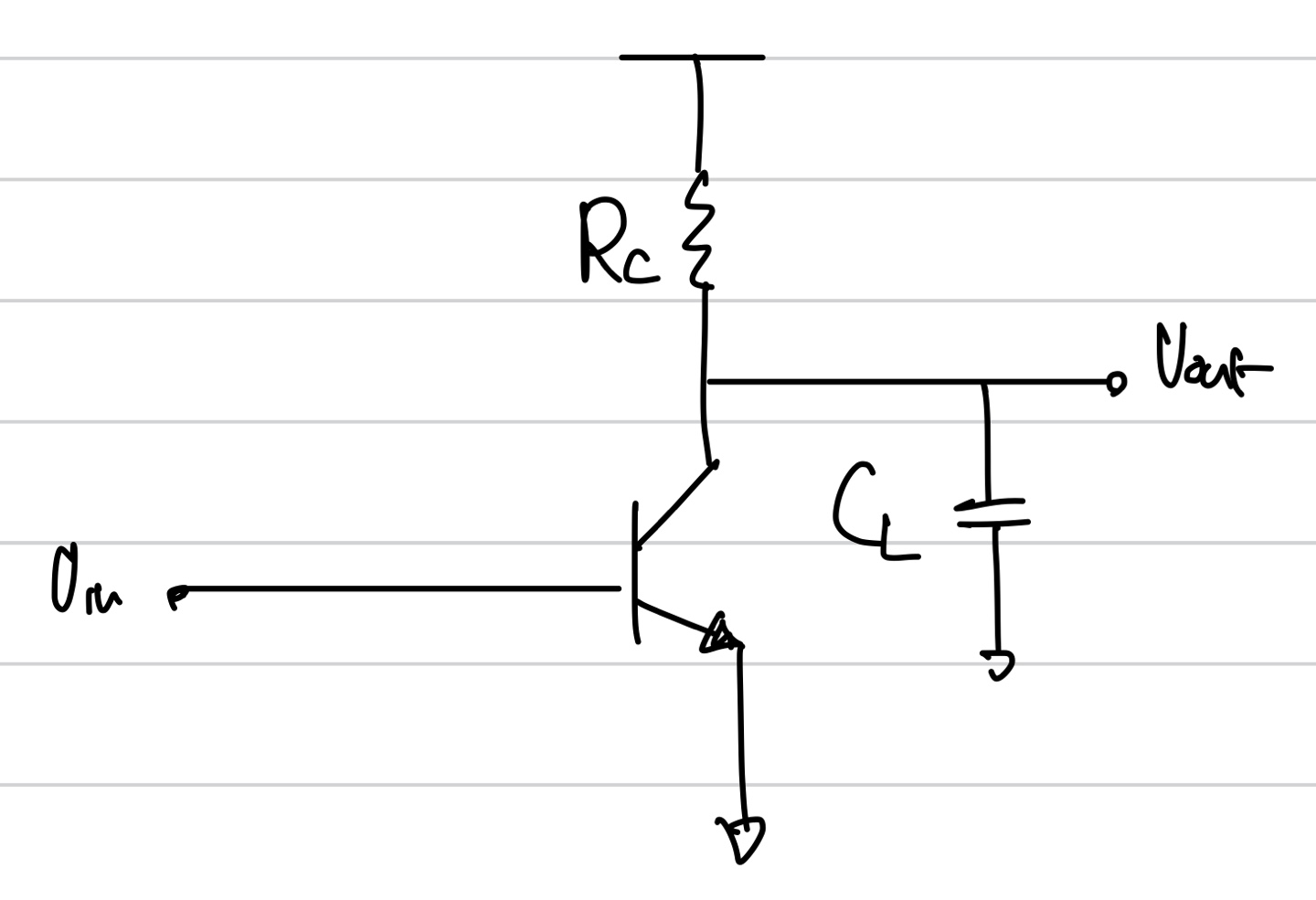
1) Rc->Rc/2가 되면 어떨까?? Ic가 일정하다고 가정하자.
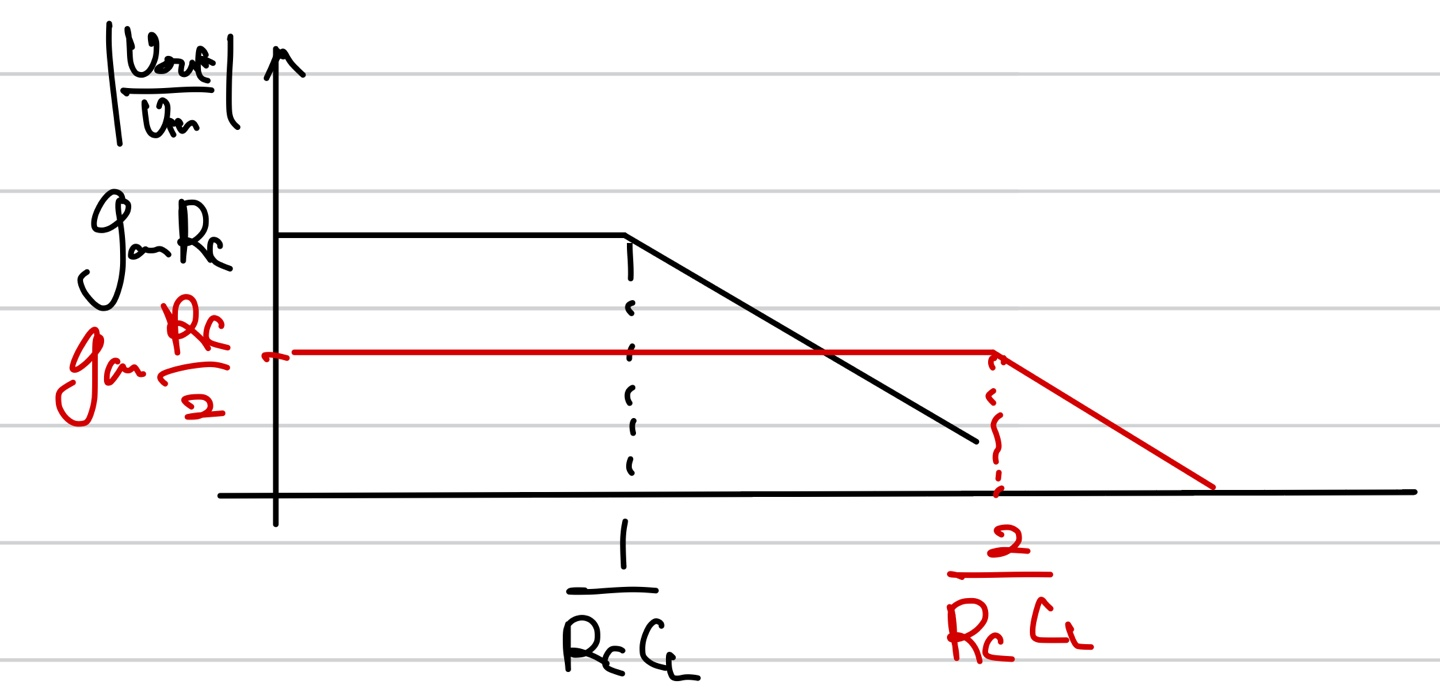
pole inspection을 통해 Vout에 pole이 존재하고 이를 구하면 1/RC이다. 현재 저항의 값을 반으로 줄이게 되면 pole의 값이 두배로 늘어나고 gain은 반으로 줄어들게 된다. 그 결과 위와 같이 bandwidth가 늘어나게 된다. 여기서 다시 한번 gain과 bandwidth의 tradeoff를 확인할 수 있고 이 두 값을 곱해보면

일정한 값이 나옴을 알 수 있다. 전류의 값 또한 일정함으로 위의 식을 통해 다시한번 gain과 BW가 trade off 관계임을 알 수 있다.
2) Rc->Rc/2로 전류는 두배로 늘려보자.
gm의 값을 bipolar의 경우로 생각을 하면 Ic/Vt임으로 전류가 두배로 늘어나면 gm도 두 배가 된다. 그리고 저항의 값이 반으로 감소했으므로 gain이 일정하게 된다. 그러나 기존의 pole의 값이 저항의 값이 반으로 감소하면서 2배 늘어나게 되고 그 결과 아래와 같이 나타나게 된다.
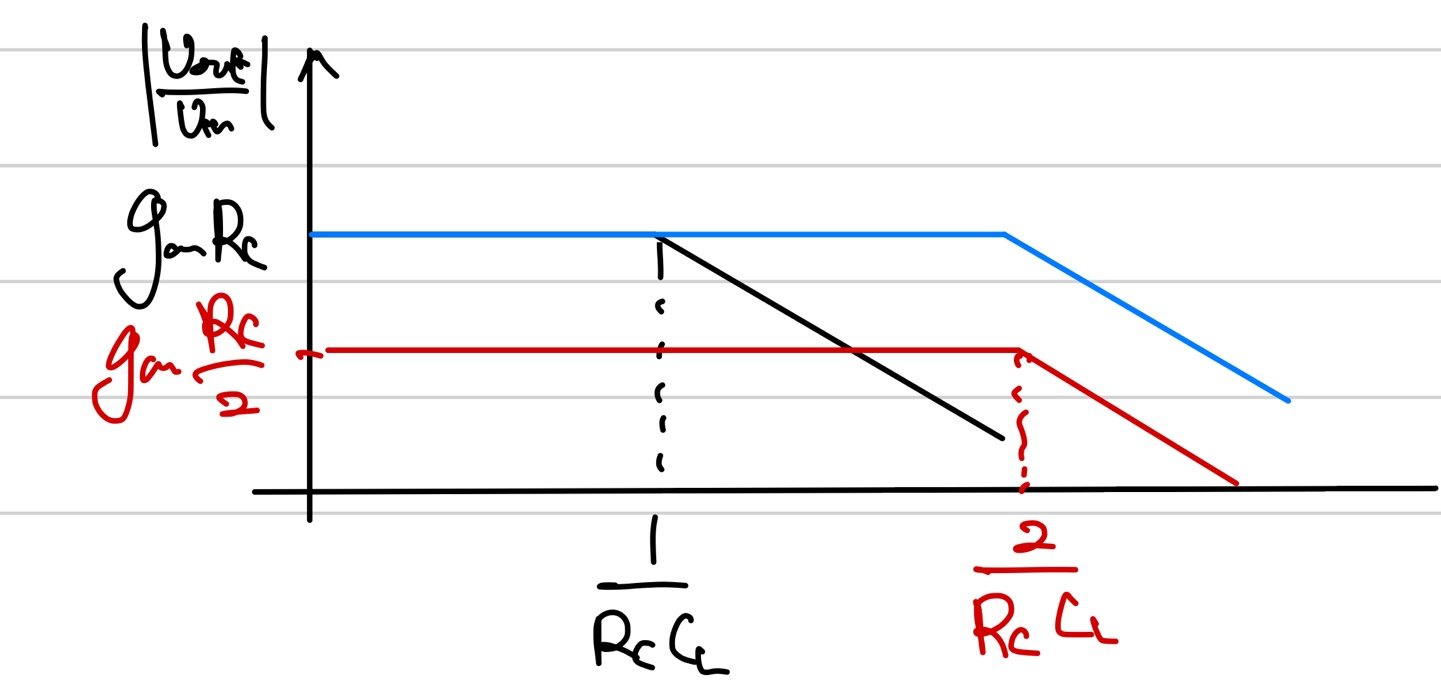
이를 바탕으로 아래와 같은 관계를 생각할 수 있다.

gain과 BW의 tradeoff 관계는 이전에 살펴보았는데 이번에는 전류의 값을 증가시켜서 gain의 값을 일정하게 유지시켰다. 그 결과 power consumption이 증가하게 되었다.
요약하자면 gain과 BW는 기본적인 상관관계가 있는데 여기서 전류의 값이 증가하게 되면 gain이 더 증가하지만 그에 따라 전력의 소모가 증가하게 되는 단점이 존재하게 된다.
V/R
윤.
'윤. 전기전자 > Frequency Response' 카테고리의 다른 글
| Lecture 24. Response of Emitter/ Source Followers, Input & Output impedance (0) | 2021.07.27 |
|---|---|
| Lecture 23. Examples of High-Speed Circuits, Response of Common Base/Gate stage (0) | 2021.07.27 |
| Lecture 21. Computation of Freq. Resp, Freq.Resp of Common Emitter/Source Stage (0) | 2021.07.26 |
| Problems (0) | 2021.07.26 |
| Examples (0) | 2021.07.22 |




댓글 영역