고정 헤더 영역
상세 컨텐츠
본문
CE Degeneration 의 몇 가지 예시를 우선 하고 넘어가자.
EX)

Rout을 구해보자. 여기서 R1만 없으면 단순히 앞 서구 한 Rout인

하지만 여기서는 R1이 collector에서 emitter로 연결되어 있다. 이는 ro와 비슷한 구조이다. 즉 R1과 ro가 parallel하게 연결되어 있음을 예상해 볼 수 있다. 그럼 small signal model을 그려보면

ro와 R1이 병렬로 연결된 상태임을 다시한번 확인할 수 있다. 이를 통해 ro에 R1이 병렬로 연결된 하나의 저항으로 생각하면 아래와 같은 결과를 얻을 수 있다.

EX)
이번에는 constant current source을 emitter에 연결했을 때를 보자.

Small signal model에서 I1은 open 상태로 된다. 즉 Re가 무한대가 됨으로 이를 고려하면 아래와 같이 식을 쓸 수 있다.

보통 rpi가 (beta+1)ro보다는 작기 때문에 beta*ro로 생각해 줄 수 있다.
-Introduction to Biasing
이제 제대로 biasing에 대해 알아보자. 우선 우리가 지금까지는 아래와 같이 biasing을 해주었다.

그럼 이렇게 두개의 전압원을 사용하지 않고 공급해줄 방법이 뭐가 있을까???
그래서 voltage divider로 Vcc를 나누어 Vo를 base에 공급해 줄 수 있다.

근데 위의 식에서 하나 생각해 볼 점이 있다. 바로 base 전류이다. 원래 voltage divider를 생각하면 두 저항에 전류의 값이 같아야 한다. 근데 여기서는 base에 전류가 흐르면서 R2에 흐르는 전류의 값이 R1과 달라진다.

그럼 위의 초록색으로 하이라이트 한 부분을 thevinen circuit를 이용해 간단하게 생각해보자.

그럼 Thevinen voltage는 R2의 전압이고 Thevinen resistor구하면 R1과 R2가 Vcc=0이면 병렬임으로 이를 이용해 아래의 회로를 생각할 수 있다.

위의 회로에서 KVL을 적용하면 아래와 같이 식을 정리할 수 있다.

그럼 우리가 Vx에서 원하는 값을 얻으려면 Ib의 값이 무시할 정도로 작으면 된다.
이제 두가지에 대해 생각해보려 한다.
1) input impedance는 변화가 있는지 알아보자.
small signal model에서는 Vcc가 AC GND가 된다. 그렇게 되면 R1이 AC GND로 R2는 애초에 GND로 아래와 같은 small signal model을 생각할 수 있다. 이 그림을 보기 전에 R1과 R2가 GND에 모두 연결되어 있고 rpi가 base에는 존재함으로 이들이 병렬로 연결되어 있을 것이라는 생각을 할 줄 알면 좋을 것 같다.

위의 그림에서와 같이 다시 한번 확인해 볼 수 있다.
그럼 이를 계산하면 Rin은 세 개의 저항을 병렬로 연결한 형태로 나오게 될 것이다. Rin의 값이 낮아지게 된다. 그런데 ideal amplifier의 조건에서 Rin이 매우 커야 되는데 이렇게 낮아지면 오히려 손해가 된다.

그래서 R1과 R2를 매우 크게 해서 rpi에 영향을 안 미치게 해야 한다.
2) 그럼 이 biasing 된 회로를 어떻게 연결해야 할까?
아래와 같이 다른 임의의 amplifier를 연결시킨다고 가정하면

Vx의 전압에 따라 앞의 transistor의 collector 전압이나 다른 조건을 만족시킬 수도 아님 만족하지 못해 의도한 값을 못 구할 수 도 있다.
a) Vout이 0.8V로 Vx와 같으면 문제없이 연결시켜주면 된다. 이를 DC Coupling이라고 한다.
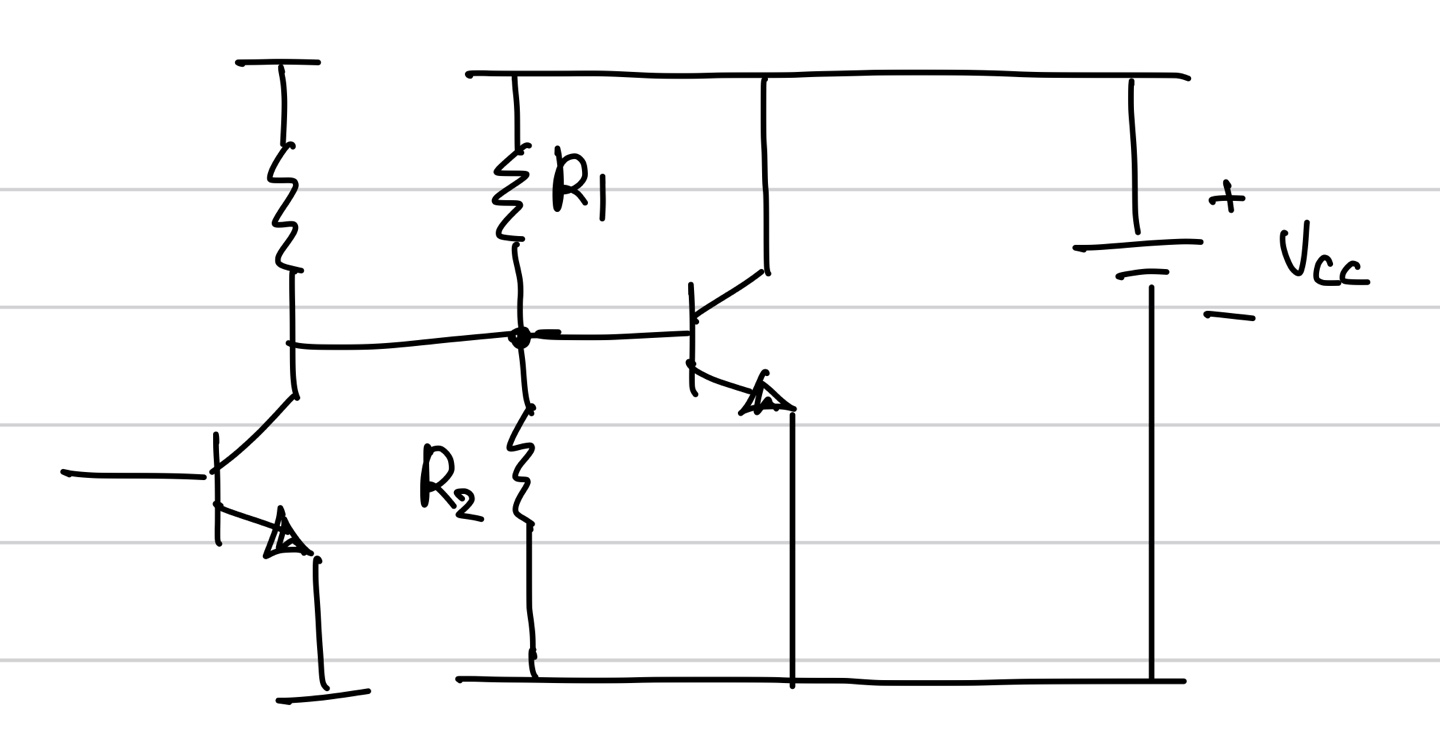
b) Vout이 Vx와 전압이 다를 때는 어떻게 해야 할까??
이를 AC Coupling이라 부른다. 바로 capacitor를 사용한다.
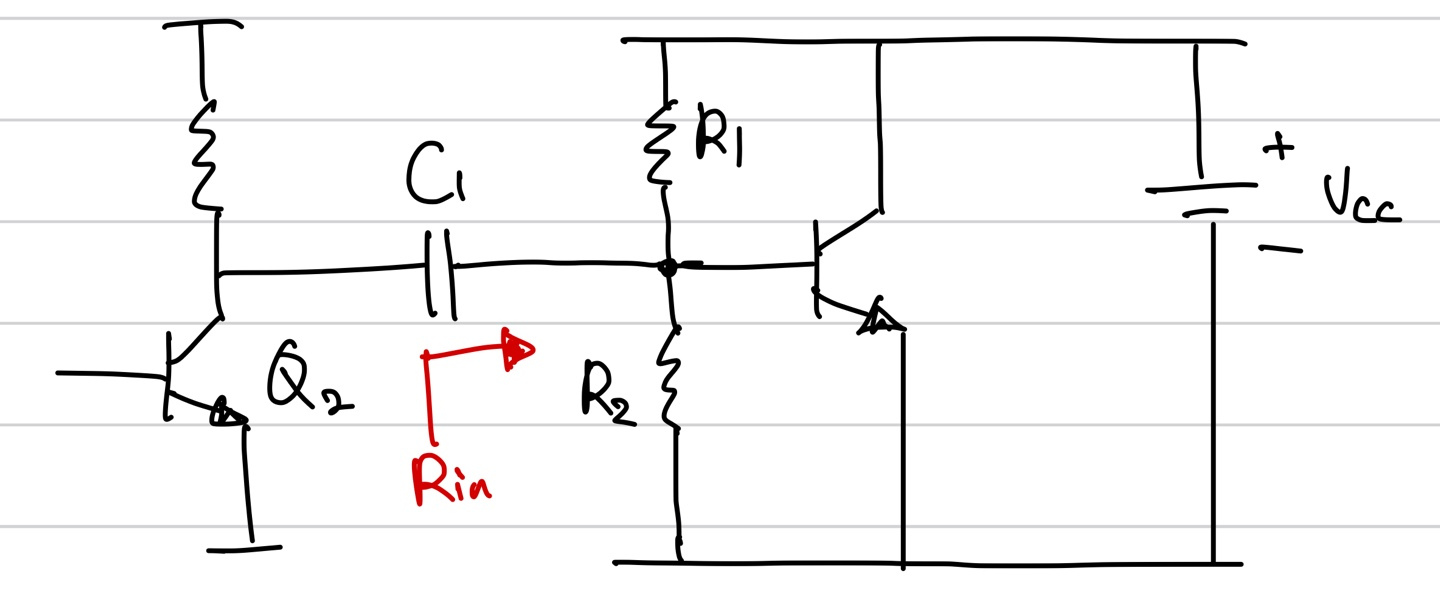
cap의 주파수에 따른 반응을 이용했다. DC만 있을 때는 open 상태로 서로가 영향을 미치지 못하지만 AC에서는 C1이 short 상태가 되면서 통과될 수 있다. 즉 small signal만이 통과하여 원하는 목표를 서로에게 영향을 미치지 않고 이룰 수 있다. 이때의 C1의 값이 signal의 최소의 주파수에서 short 상태가 되어야 한다. 왜냐하면 C1의 임피던스 값이 Q2의 collector의 Rout 값과 bias 된 회로의 Rin의 값에 영향을 미칠 수 있다. 적어도 확실한 거는 C1의 임피던스 값이 기존의 Rin의 값보다는 매우 작아서 영향을 미치지 않게 해야 한다.
-Problem Supply Sensitivity
Vcc가 5% 커졌다고 가정해보자. Vcc가 상승하면 R1 R2의 비로 Vb의 값이 증가하고 그로 인해 Vbe도 5% 증가한다. 이러한 경우를 생각하는 이유는 현실에서 Vcc가 일정하지 않을 수도 있기 때문이다. 배터리가 오래돼서 Vcc가 감소한다던지 등등의 이유로 Vcc가 바뀔 수 있는데 이와 같은 변수를 위해 무엇을 해야 하는지 알아보자.
Vcc가 800mV라고 가정하면 5%상승하면 Vbe가 40mV 상승한다. 이렇게 되면 예전에 이야기한 것처럼 60mV당 Ic가 10배 증가하듯이 40mV 증가하면 4.65배 증가하게 된다. 이렇게 되면 bias가 당연히 깨지게 된다.
정답을 이야기하자면 Degeneration을 이용해 Vcc에 대한 sensitivity를 줄일 수 있다.

우선 이에 대해 생각해 보기 전에 base의 전압을 올리면 Re의 전압도 오를까??
Re의 전압이 일정하다고 가정하면 base의 전압이 상승하면 Vbe의 값이 증가하게 된다. 그 결과 전류가 더 많이 흐르게 되고 그렇게 되면 Re의 전압이 상승할 수밖에 없다. 모순이 발생함으로 base의 전압 변화로 인해 emitter에도 전압의 변화가 발생할 것이다. 그럼 변화량이 같을까?? 같지 않다. 그래서 base 의 전압이 변해도 emitter의 전압도 변하기 때문에 Vbe의 값이 base에서의 변화보다 적게 변화한다. 즉 앞서 나온 4.65배만큼의 변화는 나타나지 않고 이보다 더 작은 값으로 나타날 것임을 예상해 볼 수 있다.
V/R
윤.
'윤. 전기전자 > Biploar Transistor' 카테고리의 다른 글
| Lecture 26. Common-Base Stage (0) | 2021.01.24 |
|---|---|
| Lecture 25. Biasing Techniques 2 (1) | 2021.01.21 |
| Lecture 23. More on Emitter Degeneration (0) | 2021.01.19 |
| Lecture 22. Common-Emitter with Degeneration (0) | 2021.01.19 |
| Lecture 21. Input & Output Impedance (0) | 2021.01.18 |




댓글 영역