고정 헤더 영역
상세 컨텐츠
본문
-illustrative Example
-> ideal하지 않은 경우에 Closed Loop Gain을 구해보자.
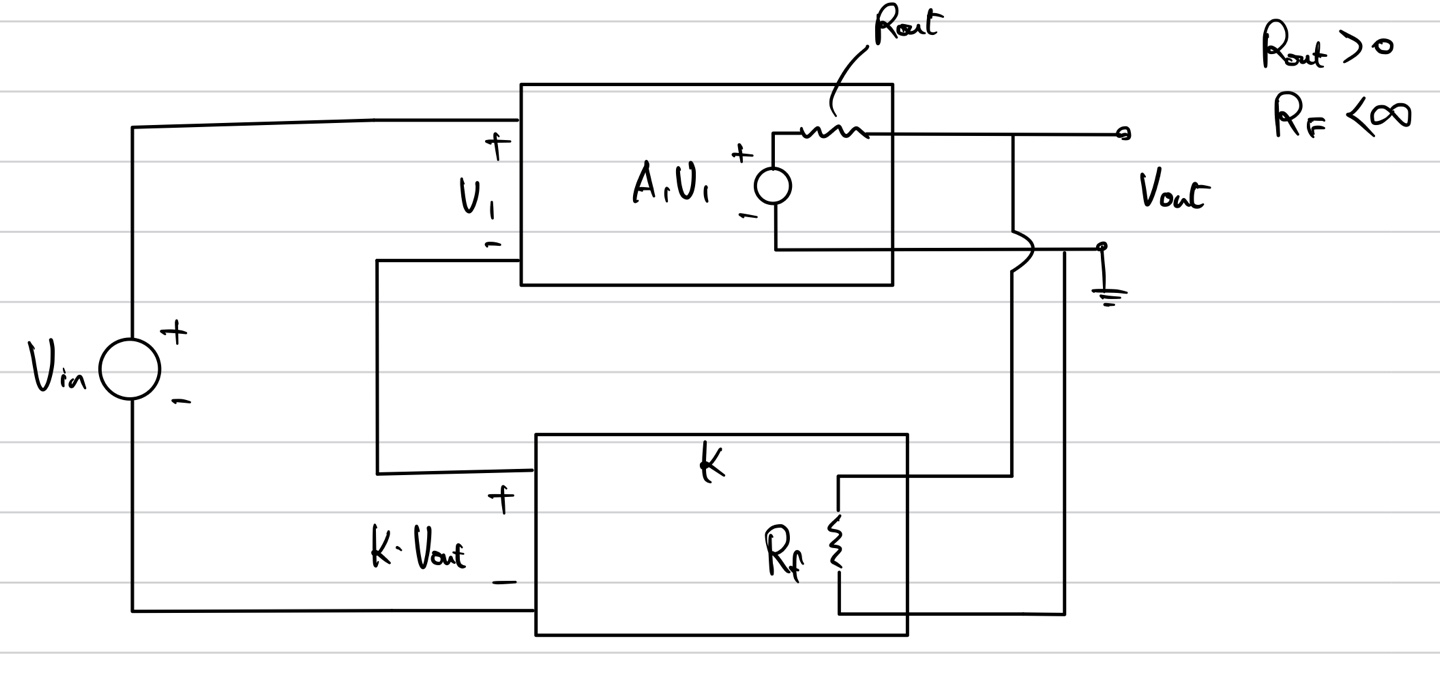
이전에는 Rout은 0 Rf는 무한대였지만 이제는 아니다. Rf에는 Vout가 parallel(Shunt) 하게 연결되어 있으므로 전압의 값이 Vout이 된다. 그 결과 U(feedback signal)의 값은 K*Vout이 된다. KVL을 하면 V1의 값을 구할 수 있다. 이제 Vout을 구하면 Vout/Vin을 구할 수 있는데 이를 자세히 보면 아래와 같은 관계이다.

Rf와 Rout은 Voltage divider로 작용함으로 이를 이용해 구하면 위와 같은 결과를 얻을 수 있다. 여기서 우리는 기존의 A1/(1+K*A1)의 꼴을 만족시키기 위해서 Open Loop Gain의 값이 변했다고 생각을 한다.
-Open the Loop Properly
이전 글에서 말했듯이 Loop Break를 할 때 문제가 있음을 확인하였다. 그래서 우리는 아래와 같이 Loop Break를 한다.

K(Feedback Factor)를 복제하여 위와 같이 만들어 생각을 한다.
EX)
실제 Transistor에서 구현하면 아래와 같다.

K를 복제하여 두개를 만들고 위와 같이 해주면 된다. 이때 BJT에 붙어있는 R1과 R2의 경우 Vout에서 Loop Break 한 것과 같이 되고 Vout에 붙어있는 R1과 R2는 BJT와 끊어진 것임으로 중간에 Loop Break가 된 것으로 그려진다.
위와 같이 Loop Break한 부분을 Open 상태로 두는 게 아니라 아래의 표에 따라 연결을 해준다.
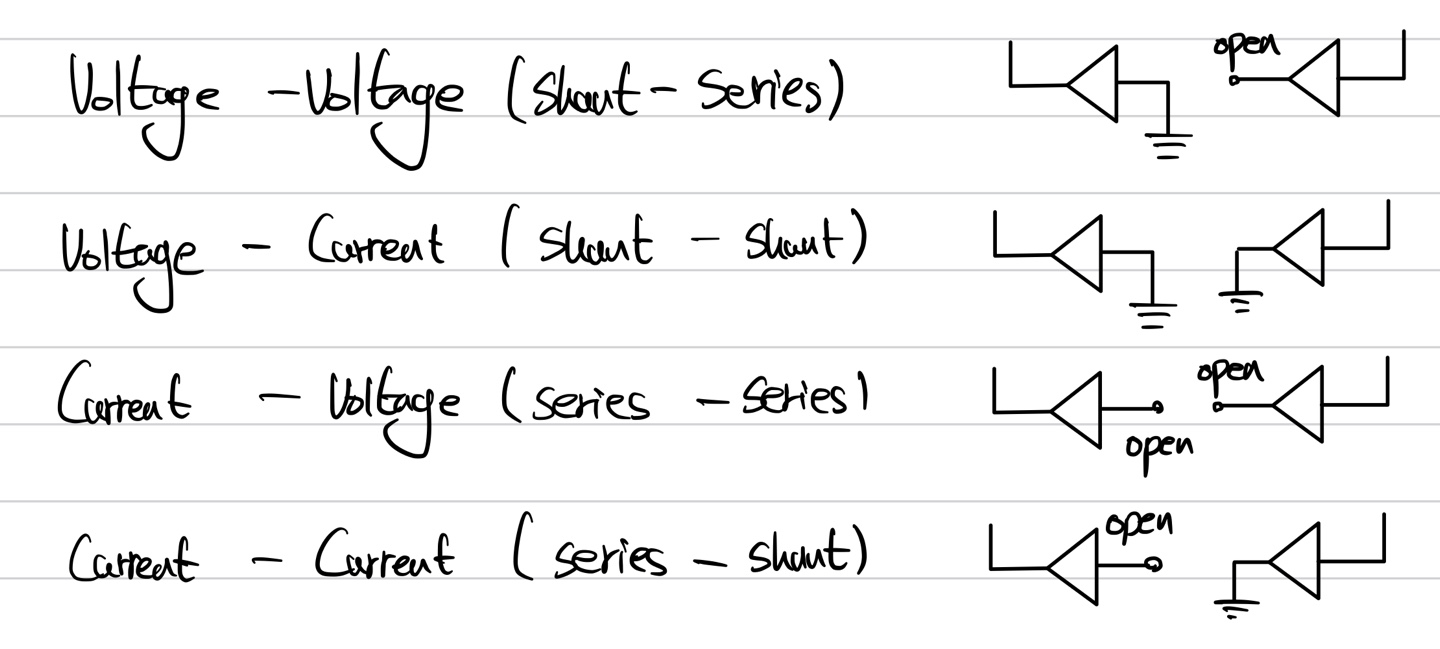
정확히 이러한 결과를 구하지는 않는다. 그저 외우기 편하게 하려면 Voltage-Voltage의 경우 Av의 Rout이 매우 작다. 그래서 왼쪽에 copy 된 k에는 GND를 연결해주고 Av의 Rin은 매우 커야 됨으로 오른쪽 k의 경우 open 상태로 해준다고 생각하면 좋다. Current-Voltage의 경우 Av의 Rout이 매우 커야 됨으로 왼쪽 K에는 OPEN 그리고 Av의 Rin도 전압 sense를 위해 매우 커야 하므로 오른쪽 K가 OPEN이 된다. 이런 식으로 생각하면 위의 관계를 직관적으로 이해할 수 있다.
EX)

위의 회로는 앞서 배운 회로이다. 이제 제대로 Loop Break를 해서 분석해보자.

위와 같이 K를 복제해서 만들어주었는데 왼쪽 K의 경우 원래 Vout과 연결되어 있으므로 R1의 위에를 오른쪽 K의 경우 base에 연결되어 있었으므로 R1과 R2 사이를 break해준다. 위의 Feedback system은 Voltage-Voltage임으로 앞서 표에서 본 것처럼 왼쪽의 K는 GND를 오른쪽 K는 OPEN상태로 해준다.
이 상태에서 Open Loop gain을 구할때 base의 저항의 값은 어차피 gain에 영향을 별로 주지 않으므로 Rc와 parallel 하게 있는 R1+R2를 고려해야 한다.

이제 Open loop Rin과 Rout을 구해보면 아래와 같다.

위의 값들은 전자회로1 내용을 참고해서 바로 구할 수 있다. 그래서 복습 중요...
BJT의 Base에서 R1과 R2가 parallel 하게 있고 이전에 배웠듯이 Emitter에서 R1||R2는 beta+1로 나눈 것만큼으로 보이게 된다.
EX)

이번에는 gain을 높이기 위해 stage를 늘린 회로이다. 이제 배운것처럼 Loop Break를 해보면

이번에도 Voltage-Voltage feedback임으로 왼쪽은 GND 오른쪽은 OPEN으로 해준다. 우선 Open Loop Gain을 구해보면 이는 Vx를 이용한다.
Vout/Vin=Vx/Vin*Vout/Vx를 이용해 구한다.

Vout/Vx를 구해보면 -gm2*Rout임을 쉽게 알 수 있다. 그러면 Vx/Vin을 생각해보자. CE stage인데 K가 하나 더 있으면서 R1||R2가 emitter degeneration으로 작동함을 알 수 있다. 그래서 위와 같이 식을 세우게 된다. 그리고 위의 회로는 BJT임으로 Rpi가 있으므로 이를 고려하여 식을 구해야 한다.
Open Loop input/output impedance를 구하면 아래와 같다.

Emitter Degeneration은 base에서 보일때는 beta+1 만큼 증폭되어 나타나게 된다.
이제 K를 구하려고 하니 Emitter와 R1+R2가 연결되어 있으므로 이를 고려해야 되나??라는 생각이 들 수 있다. 하지만 Open Loop parameter를 구할때 이를 고려하였으므로 또 구할 필요 없다. 예를 들면 위의 회로에서는 K=R2/R1+R2이다. 이에 대해서는 자중에 다시 살펴보자.
EX)

이번에는 Voltage-Current feedback임으로 이를 다시 한번 Loop Break 하여 분석해보자.

Rf가 copy된 K이다. Av가 TIA임으로 Rout이 작은 값이고 Rin도 current sense 하기 위해서 작은 값임으로 Rf에 모두 GND를 연결해준다.
이제 Open Loop Gain을 구하면

위와 같은 방식을 이용하려 한다. 우선 Vx/Iin을 구해보자. Iin의 전류가 Rf와 Q1으로 나눠짐으로 이를 Current divider로 이용해 구하면 아래와 같다.

Vout/Vin은 CE stage임으로 아래와 같다.

이 두 값을 곱하여 Open Loop Gain을 구하면 아래와 같다.

Open Loop input/output impedance는 아래와 같다.

EX)

우리가 Loop Break의 문제를 발견한 TIA 회로이다. 이를 Loop Break하면 아래와 같다.

Voltage-Current feedback임으로 Rf에 모두 GND를 연결한다. Open Loop Gain을 구해보면 아래와 같다.

V/R
윤.




댓글 영역